Konsep dan Contoh Soal Rangkaian Kapasitor dan Jenis-Jenis Kapasitor - Fisika SMA Kelas 12

Kapasitor merupakan suatu komponen elektronika yang mampu menyimpan muatan listrik. Kapasitor tersusun dari dua buah konduktor (elektroda) yang saling berdekatan tetapi tidak bersentuhan satu sama lain. Hampir semua rangkaian elektronika memanfaatkan kapasitor, suatu komponen yang juga biasa disebut sebagai kondensator. Muatan listrik disimpan di dalam kapasitor untuk digunakan pada saat tertentu contohnya adalah untuk menyalakan lampu flash kamera. Kapasitor juga dimanfaatkan dalam proses backup energi pada beberapa peralatan (device), seperti komputer, jika terjadi putusnya aliran listrik. Selain itu, kapasitor juga mampu menahan lonjakan muatan dan energi listrik agar tidak merusak rangkaian.

Diantara dua elektroda pada kapasitor, terdapat jarak pemisah atau sekat bahan isolator yang disebut sebagai dielektrik. Nah berdasarkan bahan dielektrik atau isolator, terdapat jenis-jenis kapasitor yang ada di pasar komponen elektronika, yaitu: kapasitor keramik, kapasitor polyester, kapasitor kertas, kapasitor mika, kapasitor elektrolit, dan kapasitor tantalum. Karena begitu pentingnya kapasitor dalam beberapa aplikasi elektronika di atas, maka pada materi fisika SMA Kelas 12 ini akan dibahas topik-topik tentang kapasitor, yaitu:
(a) kapasitansi kapasitor
(b) konsep dielektrik
(c) rangkaian kapasitor
(d) energi yang tersimpan dalam kapasitor

1. Kapasitansi Kapasitor

Ilustrasi Model dan Simbol Kapasitor

Stuktur paling sederhana dari suatu kapasitor adalah berupa keping atau plat sejajar yang masing-masing memiliki luas penampang $A$ dan terpisah sejauh $d$ seperti Gambar a di atas. Dalam beberapa aplikasi, proses fabrikasi menggulung plat sejajar tersebut sehingga berbentuk silinder seperti Gambar b. Berdasarkan stuktur dasar kapasitor yang berupa dua plat sejajar, maka simbol kapasitor berupa dua garis sejajar sama panjang.

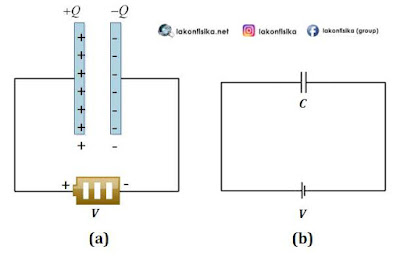Ilustrasi Proses Charging Kapasitor

Jika dua kutub sumber tegangan dihubungkan dengan kapasitor seperti gambar di atas, maka muatan listrik mengalir dari baterai menuju masing-masing plat kapasitor. Akibatnya satu plat akan mendapat muatan positif dan satu yang lain mendapat muatan negatif. Pada kondisi seperti ini, kapasitor akan mendapatkan muatan sebesar $Q$ yang besarnya sebanding dengan beda potensial antara dua plat yaitu $V$. Hubungan keduanya dinyatakan dalam persamaan 1 berikut ini.

$Q=C\,V\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$ 

Pada persamaan 1, konstanta $C$ inilah yang disebut sebagai kapasitansi. Kapasitansi merupakan suatu konstanta yang menyatakan kemampuan kapasitor untuk menyimpan muatan. Satuan kapasitansi dinyatakan dalam satuan Farad $\left( F \right)$. Beberapa kapasitor yang ada di pasaran memiliki nilai kapasitansi atau kapasitas dalam rentang $1\,pF$ $\left( picofarad={{10}^{-12}}F \right)$ sampai $1\,\mu F$ $\left( mikrofarad={{10}^{-6}}F \right)$. 

Ketika kapasitor mengalami proses charging, dibutuhkan usaha untuk memindahkan muatan listrik sebesar $Q$ menuju plat kapasitor. Sehingga terjadi perubahan potensial listrik pada plat kapasitor sebesar $V$. Besar usaha sebanding dengan beda potensial rata-rata antara dua plat, yaitu $\frac{V}{2}$. Setelah proses charging berhenti (atau jalur dengan sumber tegangan diepas), usaha saat proses charging tersebut disimpan dalam bentuk energi listrik oleh kapasitor. Besar energi yang tersimpan dalam kapasitor adalah:

$E\ \ =\ \ \frac{1}{2}QV\ \ =\ \ \frac{1}{2}C{{V}^{2}}\ \ =\ \ \frac{1}{2}\frac{{{Q}^{2}}}{C}\quad \ldots \ldots \ldots \ldots \ldots \left( 2 \right)$ 

Hal esensial yang perlu dipahami dari persamaan 1 yaitu nilai $C$ tidak bergantung nilai $V$ dan $Q$. Kapasitansi ditentukan berdasarkan proses fabrikasi atau pembuatan kapasitor yaitu bergantung pada luas penampang plat $\left( A \right)$, jarak antar plat $\left( d \right)$, dan material dielektrik yang digunakan. Hubungan besaran-besaran tersebut dinyatakan dalam persamaan 3 berikut.

$C={{\varepsilon }_{o}}\frac{A}{d}\quad \ldots \ldots \ldots \ldots \ldots \left( 3 \right)$ 

Nilai ${{\varepsilon }_{o}}$ merupakan permitiviitas ruang hampa, yang digunakan jika diantara plat tidak ada material dielektrik atau hanya ada udara $\left( {{\varepsilon }_{0}}=8,85\times {{10}^{-12}}\,{{{C}^{2}}}/{N\cdot {{m}^{2}}}\; \right)$. Jika di daerah dielektrik di pasang material tertentu maka nilai kapasitansi dinyatakan dalam persamaan 4, dengan $\kappa $ adalah koefisien bahan dielektrik.

$C=\kappa {{\varepsilon }_{o}}\frac{A}{d}\quad \ldots \ldots \ldots \ldots \ldots \left( 4 \right)$

Contoh Soal Kapasitansi Kapasitor

(1). Sebuah kapasitor plat sejajar memiliki ukuran masing-masing plat adalah $20\,cm\ \times \ 3\,cm$ yang terpisah udara sejauh $1\ mm$. Kapasitor dihubungkan dengan baterai $12\ volt$. Tentukan:

(a) kapasitas kapasitor tersebut,

(b) muatan yang tersimpan dalam kapasitor,

(c) medan listrik antara kedua plat,

(d) luas penampang plat jika kapasitansi ingin dijadikan $1F$ dan jarak kedua plat semakin rapat menjadi $10\ \mu m$.

Jawab:

(a) dengan ukuran plat $20\,cm\ \times \ 3\,cm$, maka $A=6\cdot {{10}^{-3}}\ {{m}^{2}}$

$C={{\varepsilon }_{o}}\frac{A}{d}$ 

$C=8,85\cdot {{10}^{-12}}\frac{6\cdot {{10}^{-3}}}{1\cdot {{10}^{-3}}}$

$C=53,1\cdot {{10}^{-12}}F=53,1\ pF$

(b) dengan $V=12\,volt$, maka:

$Q=C\,V$ 

$Q=\left( 53\cdot {{10}^{-12}} \right)\left( 12 \right)$

$Q=6,4\cdot {{10}^{-12}}C$

(c) kita asumsikan medan listrik di antara kedua plat bersifat homogen

$E=\frac{V}{d}$ 

$E=\frac{12}{1\cdot {{10}^{-3}}}=1,2\cdot {{10}^{4}}\,{N}/{C}\;$

(d) nilai $C=1F$ dan $d=10\mu m={{10}^{-5}}m$ 

$C={{\varepsilon }_{o}}\frac{A}{d}$ 

$A=\frac{C\,d}{{{\varepsilon }_{o}}}$ 

$A=\frac{\left( 1 \right)\,\left( {{10}^{-5}} \right)}{8,85\cdot {{10}^{-12}}}\approx 1,1\cdot {{10}^{5}}\,{{m}^{2}}$

(2). Perangkat lampu flash kamera menyimpan energi dalam kapasitor $660\ \mu F$ dengan tegangan $330\ volt$. 

(a) Berapakah energi yang mampu disimpan oleh perangkat tersebut?

(b) Berapakah daya output jika seluruh energi dilepaskan dalam waktu $1\ ms$? 

Jawab:

(a) Nilai $C=660\ \mu F=66\cdot {{10}^{-5}}F$ dan $V=330\text{ V}$, energinya adalah:

$E=\frac{1}{2}C{{V}^{2}}$ 

$E=\frac{1}{2}\left( 66\cdot {{10}^{-5}} \right){{\left( 330 \right)}^{2}}$

$E\approx 36\ J$

(b) waktu pelepasan energi adalah $t=1\ ms={{10}^{-3}}s$, daya outputnya adalah:

$P=\frac{E}{t}$ 

$P=\frac{36}{{{10}^{-3}}}=36\cdot {{10}^{3}}\ Watt=36\ kW$

(3). Dua plat kapasitor awalnya terpisah medium udara satu sama lain. Kapasitor tersebut dalam kondisi terisi penuh muatan listrik. Saat diukur dengan voltmeter, beda potensial kedua plat adalah $85\ V$. Pada kondisi yang sama, jika di antara dua plat disisipkan bahan dielektrik, beda potensialnya turun menjadi $25\ V$. Berdasarkan fakta tersebut, tentukan nilai konstanta dielektrik $\left( \kappa  \right)$ bahan tersebut!

Jawab:

Muatan tanpa bahan dielektrik $\left( {{Q}_{a}} \right)$ =   muatan dengan bahan dielektrik $\left( {{Q}_{b}} \right)$ 

${{Q}_{a}}={{Q}_{b}}$ 

${{C}_{a}}\ {{V}_{a}}={{C}_{b}}\ {{V}_{b}}$ 

$\left( {{\varepsilon }_{o}}\frac{A}{d} \right)\left( 85 \right)=\left( \kappa {{\varepsilon }_{o}}\frac{A}{d} \right)\left( 25 \right)$ 

$85=\kappa \cdot 25$ 

$\kappa =\frac{85}{25}=3,4$

2. Rangkaian Kapasitor (Rangkaian Seri Paralel)

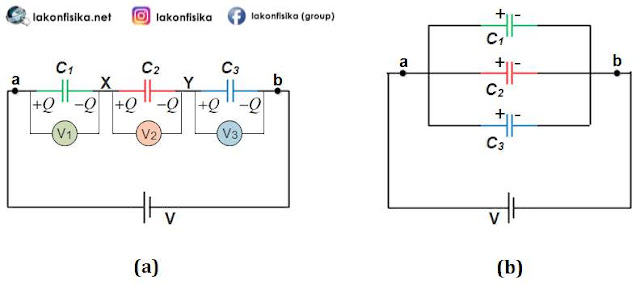
Pada suatu rangkaian elektronika, pasti tidak hanya ada satu buah kapasitor, tetapi ada beberapa susunan kapasitor. Susunan atau rangkaian dasar kapasitor terdiri dari dua jenis, yaitu rangkaian seri dan rangkaian paralel. Gambar di atas menunjukkan masing-masing rangkaian seri dan rangkaian paralel kapasitor.

Gambar a menunjukkan rangkaian seri dari 3 buah kapasitor. Ketiga kapasitor dirangkai dengan menyambung ujung-ujung kapasitor dalam satu jalur yang sama. Muatan $+Q$ mengalir dari baterai menuju satu plat kapasitor ${{C}_{1}}$, sedangkan muatan $-Q$ mengalir menuju satu plat kapasitor ${{C}_{3}}$. Muatan negatif pada plat ${{C}_{1}}$ menarik muatan positif pada plat ${{C}_{2}}$, begitu pula pada kapasitor ${{C}_{2}}$ dan ${{C}_{3}}$. Hal ini menyebabkan daerah di antara masing-masing kapasitor (daerah A dan B) dalam kondisi netral.

Karakteristik rangkaian seri kapasitor adalah:

(a) jumlah total muatan listrik yang tersimpan dalam rangkaian adalah:

${{Q}_{s}}={{C}_{s}}\,V$ 

(b) masing-masing kapasitor menyimpan muatan yang sama

${{Q}_{1}}={{Q}_{2}}={{Q}_{3}}={{Q}_{s}}$ 

(c) ujung-ujung kapasitor memiliki beda potensial (tegangan) yang membagi tegangan total $\left( V \right)$ menjadi masing-masing bernilai ${{V}_{1}},\ {{V}_{2}},\text{ dan }{{V}_{3}}$ 

$V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}$

(d) masing-masing nilai tegangan kapasitor adalah:

${{V}_{1}}=\frac{{{Q}_{s}}}{{{C}_{1}}}\quad ;\ {{V}_{2}}=\frac{{{Q}_{s}}}{{{C}_{2}}}\quad ;\ {{V}_{3}}=\frac{{{Q}_{s}}}{{{C}_{3}}}$ 

(e) nilai hambatan pengganti kapasitor seri adalah:

$\frac{1}{{{C}_{s}}}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}+\frac{1}{{{C}_{3}}}$

Sedangkan Gambar b menunjukkan rangkaian paralel dari 3 buah kapasitor. Ketiga kapasitor dirangkai dengan menyambung ujung-ujung kapasitor dalam satu jalur yang berbeda (jalur bercabang). 

Karakteristik rangkaian paralel kapasitor adalah:

(a) jumlah total muatan listrik yang tersimpan dalam rangkaian adalah:

${{Q}_{p}}={{Q}_{1}}+{{Q}_{2}}+{{Q}_{3}}$

(b) ujung-ujung kapasitor memiliki beda potensial (tegangan) yang sama

$V={{V}_{1}}={{V}_{2}}={{V}_{3}}$

(c) masing-masing muatan yang tersimpan dalam kapasitor adalah:

${{Q}_{1}}={{C}_{1}}\,V\quad ;\ {{Q}_{2}}={{C}_{2}}\,V\quad ;\ {{Q}_{3}}={{C}_{3}}\,V$ 

(d) nilai hambatan pengganti kapasitor seri adalah:

${{C}_{p}}={{C}_{1}}+{{C}_{2}}+{{C}_{3}}$

Contoh Soal Rangkaian Kapasitor

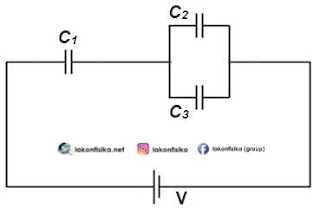
(1). Jika nilai ${{C}_{1}}={{C}_{2}}={{C}_{3}}=C$, maka nilai kapasitansi pengganti dari rangkaian kapasitor berikut ini adalah...

Jawab:

Kita tentukan dulu kapasitor paralel $\left( {{C}_{p}} \right)$ 

${{C}_{p}}={{C}_{2}}+{{C}_{3}}$ 

${{C}_{p}}=C+C=2C$

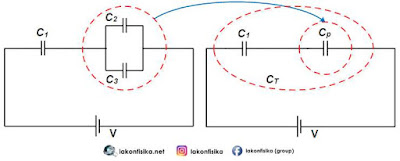
Kapasitor total $\left( {{C}_{T}} \right)$ adalah hubungan seri antara ${{C}_{1}}$ dan ${{C}_{p}}$

$\frac{1}{{{C}_{T}}}=\frac{1}{{{C}_{2}}}+\frac{1}{{{C}_{p}}}$ 

$\frac{1}{{{C}_{T}}}=\frac{1}{C}+\frac{1}{2C}$

$\frac{1}{{{C}_{T}}}=\frac{2}{2C}+\frac{1}{2C}=\frac{3}{2C}$ 

${{C}_{T}}=\frac{2}{3}C$ 

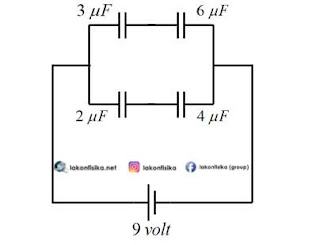
(2). Tentukan nilai kapasitansi ekuivalen dari rangkaian kapasitor berikut ini (semua kapasitansi dalam satuan mikroFarad).

Jawab:

Tahap 1:

${{C}_{p1}}=1+3=4\ \mu F$ 

${{C}_{p1}}=6+2=8\ \mu F$ 

Tahap 2:

$\frac{1}{{{C}_{s1}}}=\frac{1}{4}+\frac{1}{{{C}_{p1}}}$ 

$\frac{1}{{{C}_{s1}}}=\frac{1}{4}+\frac{1}{4}=\frac{2}{4}$ 

${{C}_{s1}}=2\ \mu F$ 

$\frac{1}{{{C}_{s2}}}=\frac{1}{8}+\frac{1}{{{C}_{p2}}}$ 

$\frac{1}{{{C}_{s2}}}=\frac{1}{8}+\frac{1}{8}=\frac{2}{8}$ 

${{C}_{s2}}=4\ \mu F$ 

Tahap 3:

${{C}_{T}}={{C}_{s1}}+{{C}_{s2}}=2+4=6\ \mu F$ 

(3). Tentukan besar energi yang tersimpan pada muatan $6\ \mu F$!

 Jawab:

Tahapan berpikirnya adalah:

a. Untuk menentukan energi pada kapasitor $6\ \mu F$, harus ditentukan muatan yang tersimpan dahulu $\left( {{Q}_{6}} \right)$, karena $E=\frac{1}{2}\frac{Q_{6}^{2}}{{{C}_{6}}}$.

b. Untuk menentukan ${{Q}_{6}}$, harus ditentukan dulu nilai ${{Q}_{s1}}$ (muatan seri 1), karena nilai ${{Q}_{6}}={{Q}_{s1}}$.

c. Untuk menentukan ${{Q}_{s1}}$, harus ditentukan nilai ${{C}_{s1}}$ dahulu, karena nilai ${{Q}_{s1}}={{C}_{s1}}\,{{V}_{s1}}$ dengan nilai ${{V}_{s1}}=V$.

Tahap 1:

$\frac{1}{{{C}_{s1}}}=\frac{1}{3}+\frac{1}{6}$ 

$\frac{1}{{{C}_{s1}}}=\frac{2}{6}+\frac{1}{6}=\frac{3}{6}$

${{C}_{s1}}=2\ \mu F$ 

Tahap 2:

${{Q}_{s1}}=\left( 2\cdot {{10}^{-6}} \right)\,\left( 9 \right)$

${{Q}_{s1}}=18\cdot {{10}^{-6}}\ C$

Tahap 3:

${{E}_{6}}=\frac{1}{2}\frac{Q_{6}^{2}}{{{C}_{6}}}$  nilai ${{Q}_{6}}={{Q}_{s1}}=18\cdot {{10}^{-6}}C$

${{E}_{6}}=\frac{1}{2}\frac{{{\left( 18\cdot {{10}^{-6}} \right)}^{2}}}{6\cdot {{10}^{-6}}}$ 

${{E}_{6}}=27\cdot {{10}^{-6}}\ J=27\ \mu J$ 

Share this post