Konsep dan Contoh Soal Kalor dan Perpindahannya - Pemuaian – Fisika SMA Kelas 11
Jul 4, 2019
Edit
Pada materi Fisika SMA Kelas 11, konsep kalor memiliki tiga topik bahasan utama yaitu konsep pemuaian, pengaruh kalor terhadap zat, dan perpindahan kalor. Untuk konsep pemuaian, terdiri dari konsep pemuaian linier (pemuaian panjang), pemuaian luas, dan pemuaian volume. Selanjutnya tentang pengaruh kalor, akan dipelajari pengaruh terhadap suhu zat dan pengaruh terhadap wujud zat. Yang terakhir akan dipelajari perpindahan kalor memalui proses konduksi, konveksi, dan radiasi. Soal pada topik-topik ini bisa dikombinasikan dengan topik fisika lainnya sehingga memenuhi karakteristik model soal HOTS fisika. Sekarang langsung saja kita pelajari bersama konsep dan contoh kalor, pemuaian, dan perpindahan kalor pada materi Fisika SMA Kelas 11.
1. Konsep Pemuaian Zat
Secara umum, zat akan mengalami pemuaian ketika dipanaskan dan akan mengerut ketika didinginkan. Seberapa besar pemuaiannya bergantung pada jenis zat tersebut. Proses pemuaian zat disebabkan adanya semakin renggangnya jarak antar atom pada zat tersebut. Jadi ketika suhu meningkat, atom-atom dalam zat tersebut akan berosilasi dengan amplitudo semakin besar, sehingga memperlebar jarak rata-rata antar atom. Ada 3 jenis pemuaian, yaitu pemuaian linier (pemuaian panjang), pemuaian luas, pemuaian volume.
Gambar a di atas menunjukkan ilustrasi pemuaian panjang. Ketika suatu batang tipis berada pada suhu awal ${{T}_{o}}$ , batang memiliki panjang awal ${{l}_{o}}$. Kemudian batang dipanaskan dan suhunya menjadi $T$ yang lebih besar dari ${{T}_{o}}$. Akibatnya, batang bertambah panjang atau memuai sebesar $\Delta l$. Jika batang dipanaskan sehingga suhu bertambah sebesar $\Delta T$, maka batang akan memuai sebesar $\Delta l$yang berbanding lurus dengan koefisien muai panjang $\alpha$ sesuai persamaan berikut:
$\Delta l={{l}_{o}}\ \alpha \ \Delta T\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
Sedangkan gambar b di atas, memberikan ilustrasi terhadap dua jenis logam yang saling menempel dan dipanaskan sehingga mengalami perubahan suhu sebesar $\Delta T$. Kuningan dan baja memiliki koefisien pemuaian yang berbeda, ${{\alpha }_{kuningan}}>{{\alpha }_{baja}}$, sehingga menyebabkan kuningan lebih cepat memuai dari pada baja. Akibatnya $\Delta {{l}_{kuningan}}>\Delta {{l}_{baja}}$, sehingga batang kuningan menekan dan berbelok (melengkung) ke arah batang baja.
Selanjutnya untuk benda yang memiliki dimensi luas, dengan luas awal ${{A}_{o}}$ dan mengalami kenaikan suhu sebesar $\Delta T$, maka benda tersebut akan mengalami pemuaian luas:
$\Delta A={{A}_{o}}\ \beta \ \Delta T\quad \ldots \ldots \ldots \ldots \ldots \left( 2 \right)$, dengan nilai $\beta =2\,\alpha$.
Jika benda mempunyai dimensi volume, maka benda dengan volume awal ${{V}_{o}}$ dan mengalami kenaikan suhu sebesar $\Delta T$, akan memuai sebesar:
$\Delta V={{V}_{o}}\ \gamma \ \Delta T\quad \ldots \ldots \ldots \ldots \ldots \left( 3 \right)$, dengan nilai $\gamma =3\alpha $.
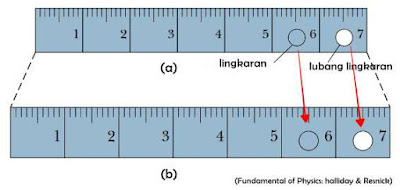
Ilustrasi lain dapat dilihat pada gambar di atas. Gambar a adalah kondisi awal penggaris dengan garis lingkaran dan lubang berbentuk lingkaran. Setelah mengalami kenaikan suhu, ternyata dimensi penggaris juga memuai, bertambah panjang dan bertambah lebar (gambar b). Garis lingkaran juga membesar begitu pula lubang lingkaran juga melebar. Hal tersebut menunjukkan terjadinya pemuaian luas pada penggaris.
Contoh Soal Pemuaian:
(1). Bantalan jembatan terbuat dari baja dan memiliki panjang 200 m pada suhu 200 oC. Kemungkinan suhu maksimum dan minimum di daerah itu adalah antara -30 oC sampai 40 oC. Berapa besar kemungkinan perubahan panjang baja tersebut? $\left( {{\alpha }_{baja}}={12\times {{10}^{-6}}}/{^{o}C}\; \right)$
Jawab:
Pemuaian terjadi saat mengalami kenaikan suhu menjadi 40 oC, sehingga nilai $\Delta T=40-20={{20}^{o}}C\\$
$\Delta l={{l}_{o}}\ \alpha \ \Delta T \\$
$\Delta l=200\ \cdot \ \left( 12\times {{10}^{-6}} \right)\ \cdot \ 20 \\$
$\Delta l=48\times {{10}^{-3}}\ m=4,8\ cm \\$
Penyusutan terjadi saat mengalami penurunan suhu menjadi -30 oC, sehingga nilai $\Delta T=-30-20=-{{50}^{o}}C\\$
$\Delta l={{l}_{o}}\ \alpha \ \Delta T \\$
$\Delta l=200\ \cdot \ \left( 12\times {{10}^{-6}} \right)\ \cdot \ \left( -50 \right) \\$
$\Delta l=-12\times {{10}^{-2}}\ m=-12\ cm \\$
Jadi perubahan panjang yang mungkin terjadi pada baja tersebut adalah 12 cm + 4,8 cm ≈ 17 cm.
(2). Sebuah tabung aluminium memiliki volume $1000\text{ }mL$ pada suhu $20{{\text{ }}^{o}}C$, dan berisi penuh gliserin. Jika suhu tabung dijadikan $120{{\text{ }}^{o}}C$ dan jika koefisien muai panjang aluminium $4\times {{10}^{-5}}{{/}^{o}}C$dan koefisien muai volume gliserin $4\times {{10}^{-4}}{{/}^{o}}C$, maka volume gliserin yang tumpah adalah ….
Jawab:
Volume yang tumpah dihitung melalui selisih pemuaian volume gliserin dan tabung aluminium.
$\Delta V=\Delta {{V}_{gliserin}}-\Delta {{V}_{tabung}} \\$
$\Delta V={{V}_{o}}\ {{\gamma }_{g}}\ \Delta T-{{V}_{o}}\ {{\gamma }_{t}}\ \Delta T \\$
$\Delta V={{V}_{o}}\ \Delta T\left( {{\gamma }_{g}}-{{\gamma }_{t}} \right) \\$
$\Delta V={{10}^{3}}\cdot \left( 120-20 \right)\cdot \left( 4\times {{10}^{-4}}-3\left( 4\times {{10}^{-5}} \right) \right) \\$
$ \Delta V={{10}^{3}}\cdot \left( 100 \right)\cdot \left( 4\times {{10}^{-4}}-1,2\times {{10}^{-4}} \right) \\$
$\Delta V={{10}^{5}}\cdot \left( 2,8\times {{10}^{-4}} \right) \\$
$\Delta V=28\text{ }mL \\$
Jadi volume gliserin yang tumpah sebesar 28 mL.
2. Konsep Kalor dan Pengaruhnya pada Benda
Pada kehidupan sehari-hari pasti kita sudah terbiasa mendengar istilah temperatur dan kalor. Nah, sekarang perlu kita pahami dulu masing-masing definisinya. Untuk memahaminya, sebenarnya kita perlu belajar dulu tentang teori kinetik gas, di dalamnya membahas energi dalam (internal energy). Energi dalam adalah seluruh energi di dalam benda yang dihasilkan oleh komponen mikroskopis benda (atom dan molekul). Yang termasuk energi dalam adalah energi kinetik dari gerak translasi atom atau molekul, gerak rotasi, getaran, dan energi potensial akibat getaran molekul serta energi potensial listrik. Selanjutnya, yang dimaksud temperatur menggambarkan derajat keterukuran energi kinetik rata-rata tiap molekul dalam benda. Jika antara dua benda atau antara sistem dan lingkungan terdapat perbedaan temperatur, maka akan terjadi aliran energi. Nah, aliran energi panas akibat perbedaan suhu inilah yang disebut sebagai kalor.
Untuk memahami konsep kalor $\left( Q \right)$, mari kita perhatikan bersama gambar di atas. Pada gambar tersebut diilustrasikan ada sistem dan lingkungan (atau bisa juga disebut sebagai benda 1 dan benda 2 yang saling berinteraksi). Sistem memiliki suhu sebesar ${{T}_{S}}$ dan lingkungan memiliki suhu ${{T}_{L}}$. Sesuai dengan pengertian kalor di atas, jika dalam suatu kondisi ${{T}_{S}}>{{T}_{L}}$ (gambar a), maka terjadi aliran kalor dari sistem menuju lingkungan (sistem melepas kalor) dan $Q$ bernilai negatif. Kemudian di gambar b, jika ${{T}_{S}}={{T}_{L}}$, maka tidak ada aliran energi panas atau $Q=0$. Selanjutnya jika ${{T}_{S}}<{{T}_{L}}$, maka terjadi aliran energi panas dari lingkungan menuju sistem (sistem menyerap kalor) dan $Q$ bernilai positif. Perlu dipahami bahwa saat sistem melepas kalor, maka lingkungan menyerap kalor tersebut, demikian pula sebaliknya. Kalor akan terus mengalir sampai terjadi kesetimbangan termal $\left( {{T}_{S}}={{T}_{L}} \right)$, dengan jumlah ${{Q}_{serap}}=-{{Q}_{lepas}}$. Inilah yang dikenal sebagai Azas Black yang sejalan dengan konsep hukum kekekalan energi, dalam hal ini adalah jumlah kalor dalam sistem selalu sama dengan nol, ada yang melepas dan ada yang menyerap kalor$\left( \sum{Q=0} \right)$.
Sekarang pertanyaannya adalah berapa besar kalor yang diserap atau yang dilepas oleh benda berwujud padat atau cair? Jadi besar kalor yang diserap atau dilepas oleh benda (sistem atau lingkungan) bergantung pada jenis zatnya, yaitu kapasitas kalor zat $\left( C \right)$ atau kalor jenis zat $\left( c \right)$. Selain itu dipengaruhi oleh perubahan suhu zat $\left( \Delta T \right)$, yaitu selisih antara suhu awal $\left( {{T}_{o}} \right)$ dan suhu akhir $\left( {{T}_{a}} \right)$ zat. Berikut ini persamaan untuk menentukan besar kalor.
$ Q=C\cdot \Delta T \\$
$ Q=C\cdot \left( {{T}_{a}}-{{T}_{o}} \right)\quad \ldots \ldots \ldots \ldots \ldots \left( 4 \right) \\$
atau dengan dengan nilai $C=m\ c$, maka:
$ Q=m\cdot c\cdot \Delta T \\$
$ Q=m\cdot c\cdot \left( {{T}_{a}}-{{T}_{o}} \right)\quad \ldots \ldots \ldots \ldots \ldots \left( 5 \right) \\$
Selanjutnya bagaimana jika terjadi perubahan wujud zat akibat kalor (yang padat melebur dan yang cair menguap)? Untuk menentukan jumlah kalor pada proses perubahan wujud zat, dapat digunakan persamaan 6 di bawah ini. Nilai $m$ merupakan massa zat, dan $L$ adalah kalor perubahan wujud zat (kalor lebur untuk proses melebur dan kalor uap untuk proses menguap).
$Q=m\cdot L\quad \ldots \ldots \ldots \ldots \ldots \left( 6 \right)$
Contoh Soal Kalor dan Perubahan Wujud Zat:
(1). Air sebanyak $20\ kg$ akan dipanaskan sampai suhu ${{90}^{o}}C$ dengan cara dimasukkan ke dalam panci yang terbuat dari besi $\left( {{c}_{besi}}=450\ J/kg\cdot {{C}^{o}}\ \text{dan }{{c}_{air}}=4200\ J/kg\cdot {{C}^{o}} \right)$. Jika panci bermassa $20\ kg$ dan suhu awalnya adalah ${{10}^{o}}C$, maka besar kalor yang dibutuhkan untuk proses tersebut adalah...
Jawab:
Perlu dipahami bahwa air dan panci memiliki suhu yang sama sebelum dipanaskan. Kalor yang dibutuhkan adalah jumlah kalor air $\left( {{Q}_{a}} \right)$ dan kalor panci besi $\left( {{Q}_{b}} \right)$.
$ Q={{Q}_{a}}+{{Q}_{b}} \\$
$ Q={{m}_{a}}\ {{c}_{a}}\ \Delta {{T}_{a}}+{{m}_{b}}\ {{c}_{b}}\ \Delta {{T}_{b}} \\$
$ Q=20\ \cdot \ 4200\ \cdot \ \left( 90-10 \right)+20\ \cdot \ 450\ \cdot \ \left( 90-10 \right) \\$
$ Q=\left( 6720\times {{10}^{3}} \right)+\left( 720\times {{10}^{3}} \right) \\$
$ Q=7440\times {{10}^{3}}\ Joule \\$
$ Q=7440\ kJ \\$
(2). Seorang insinyur ingin mengetahui kalor jenis suatu bahan campuran logam. Bahan tersebut bermassa $0,15\text{ }kg$ yang telah dipanaskan sampai suhu $540{{\text{ }}^{o}}\text{C}$. Seketika setelah dipanaskan, logam itu dimasukkan ke dalam wadah kalorimeter. Dalam wadah kalorimeter sudah berisi $0,4\text{ }kg$ air yang bersuhu $10{{\text{ }}^{o}}\text{C}$ dan wadah kalorimeter itu terbuat dari aluminium bermassa $0,2\text{ }kg$. Jika suhu akhir sistem tersebut adalah $30{{\text{ }}^{o}}\text{C}$, maka besar kalor jenis campuran logam tersebut adalah... $\left( {{c}_{al}}=900\ J/kg\cdot {{C}^{o}}\ \text{dan }{{c}_{air}}=4200\ J/kg\cdot {{C}^{o}} \right)$
Jawab:
Untuk mengerjakan soal ini, kita terapkan prinsip kekekalan aliran kalor atau azas Black.
$ \sum{Q}=0 \\ $
$ {{Q}_{logam}}+{{Q}_{air}}+{{Q}_{al}}=0 \\ $
$ {{m}_{l}}\cdot {{c}_{l}}\cdot \Delta {{T}_{l}}+{{m}_{a}}\cdot {{c}_{a}}\cdot \Delta {{T}_{a}}+{{m}_{al}}\cdot {{c}_{al}}\cdot \Delta {{T}_{al}}=0 \\ $
$ 0,15\cdot {{c}_{l}}\cdot \left( 30-540 \right)+0,4\cdot 4200\cdot \left( 30-10 \right)+0,2\cdot 900\cdot \left( 30-10 \right)=0 \\ $
$ \left( -76,5\cdot {{c}_{l}} \right)+33600+3600=0 \\ $
$ 76,5\cdot {{c}_{l}}=37200 \\ $
$ {{c}_{l}}=486,27\approx 486\ J/kg\cdot {{C}^{o}} \\ $
(3). Berapa besar energi yang harus dilepas oleh $\text{1,5 }kg$ air pada suhu $20{{\text{ }}^{o}}\text{C}$ untuk menjadi es bersuhu $-12{{\text{ }}^{o}}\text{C}$ di dalam frezer kulkas? $\left( {{c}_{es}}=2100\ J/kg\cdot {{C}^{o}}\ ;\text{ }{{c}_{air}}=4200\ J/kg\cdot {{C}^{o}}\text{ };\text{ }{{\text{L}}_{air}}=330\ kJ/kg \right)$
Jawab:
Agar lebih mudah mengerjakan soal ini, kita buat dulu diagram pengaruh kalor pada air berikut ini.
Jumlah kalor total yang dilepas adalah saat air turun suhunya $\left( {{Q}_{1}} \right)$ ditambah saat air membeku $\left( {{Q}_{2}} \right)$, dan saat sudah menjadi es dan turun suhunya $\left( {{Q}_{3}} \right)$.
$ Q={{Q}_{1}}+{{Q}_{2}}+{{Q}_{3}} \\ $
$ Q={{m}_{a}}\cdot {{c}_{a}}\cdot \Delta {{T}_{a}}+{{m}_{a}}\cdot {{L}_{a}}+{{m}_{es}}\cdot {{c}_{es}}\cdot \Delta {{T}_{es}} \\ $
$ Q=1,5\cdot 4200\cdot \left( 0-20 \right)+1,5\cdot 330000+1,5\cdot 2100\cdot \left( -12-0 \right) \\ $
$ Q=\left( -126000 \right)+\left( -495000 \right)+\left( -37800 \right) \\ $
$ Q=-658800\ J=-658,8\ kJ \\ $
Tanda negatif pada nilai kalor menunjukkan bahwa air melepas kalor ke lingkungan (freezer).
3. Konsep Perpindahan Kalor: Konduksi
Ketika kita sedang mengaduk secangkir kopi panas dengan sendok logam, ujung sendok yang kita pegang akan terasa hangat. Fenomena ini disebabkan adanya proses rambatan kalor yang disebut sebagai konduksi. Proses konduksi adalah rambatan kalor dari suatu titik dengan temperatur tinggi menuju temperatur yang lebih rendah tanpa diikuti perpindahan molekul zat perantaranya. Artinya, molekul zat perantara bergetar dan hanya saling bertumbukan untuk transfer energi, tetapi masih berada dalam posisi yang sama, atau tidak ikut mengalir bersama kalor.
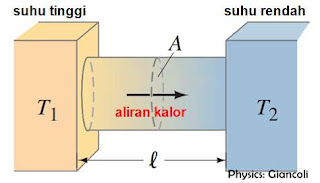
Proses konduksi diilustrasikan pada gambar di atas. Kalor mengalir dalam sebuah konduktor sepanjang $l$ dan luas penampang $A$ akibat ada perbedaan suhu pada kedua ujungnya. Kalor merambat ke kanan dari ujung yang bersuhu tinggi ${{T}_{1}}$ menuju ujung yang bersuhu rendah ${{T}_{2}}$. Rasio jumlah kalor yang mengalir tiap waktu disebut laju rambatan kalor $\left( \frac{Q}{t} \right)$ dengan persamaan 7 di bawah. Laju aliran kalor berbanding lurus dengan koefisien konduksi atau konduktivitas termal dari bahan $\left( k \right)$. Konduktivitas termal bahan merupakan kemampuan bahan untuk menghantarkan kalor, jadi semakin besar nilai $k$, maka semakin cepat kalor merambat.
$\frac{Q}{t}=k\ A\ \frac{\Delta T}{l}\quad \ldots \ldots \ldots \ldots \left( 7 \right)$
Contoh Soal Perpindahan Kalor Konduksi:
(1). Pada musim dingin, penduduk di wilayah Eropa selalu menyalakan tungku pemanas di dalam rumah. Sebagian besar kalor di dalam rumah hilang merambat ke luar rumah melalui jendela. Jendela berbahan kaca $\left( k=0,9\ {J}/{s\cdot m\cdot {{C}^{o}}}\; \right)$dengan ukuran seluas $2\,m\times 1,5\,m$ dan ketebalan $3,0\,mm$. Jika suhu di dalam rumah $15{{\text{ }}^{o}}\text{C}$ dan suhu di luar rumah $5{{\text{ }}^{o}}\text{C}$, maka besar laju aliran kalor adalah...
Jawab:
$ \frac{Q}{t}=kA\frac{\Delta T}{l} \\$
$ \frac{Q}{t}=0,9\cdot 3\cdot \frac{\left( 15-5 \right)}{3\times {{10}^{-3}}} \\ $
$ \frac{Q}{t}=9\times {{10}^{3}}\ {J}/{s}\; \\ $
(2). Masing-masing batang P dan Q memiliki ukuran yang sama, tetapi berbeda jenis logamnya. Keduanya saling didekatkan dan saling bersentuhan seperti pada gambar di bawah ini.
Jika konduktivitas termal logam P dua kali konduktivitas termal Q, maka suhu pada bidang batas P dan Q adalah...
Jawab:
Pada fenomena sambungan logam, laju konduksi pada masing-masing logam adalah sama, dengan suhu pada ujung sambungan $\left( {{T}_{x}} \right)\] juga sama.
$ {{\left( \frac{Q}{t} \right)}_{P}}={{\left( \frac{Q}{t} \right)}_{Q}} \\$
${{k}_{P}}\,{{A}_{P}}\frac{\Delta {{T}_{P}}}{{{l}_{P}}}={{k}_{Q}}\,{{A}_{Q}}\frac{\Delta {{T}_{Q}}}{{{l}_{Q}}}$ , karena ukuran sama, maka ${{A}_{P}}={{A}_{Q}}$ dan ${{l}_{P}}={{l}_{Q}}$
$ {{k}_{P}}\ \Delta {{T}_{P}}={{k}_{Q}}\ \Delta {{T}_{Q}} \\ $
$2\,{{{k}_{Q}}}\ \left( 90-{{T}_{x}} \right)={{{k}_{Q}}}\ \left( {{T}_{x}}-0 \right) \\ $
$180-2\,{{T}_{x}}={{T}_{x}} \\ $
$3\,{{T}_{x}}=180 \\$
${{T}_{x}}=60{{\ }^{o}}C \\ $
4. Konsep Perpindahan Kalor: Konveksi
Di dalam proses memasak air terdapat fenomena konveksi kalor. Perlu dipahami bahwa proses konveksi hanya terjadi pada air (yang berupa fluida), bukan proses rambatan kalor pada panci airnya. Ilustrasinya ditunjukkan pada gambar di bawah ini. Jadi ketika dipanaskan, air di bagian bawah panci akan lebih dulu panas, sedangkan air di bagian atas masih dingin. Akibat ada perbedaan suhu antara air di bagian bawah dan dia bagian atas, maka terjadi rambatan kalor. Air di bagan bawah akan merambatkan kalor ke bagian atas beserta aliran molekul airnya. Jadi proses rambatan kalor diikuti oleh molekul zat perantaranya dan inilah yang disebut sebagai proses konveksi. Proses ini akan berlangsung selama air dipanaskan, sampai air mendidih dan menguap.
5. Konsep Perpindahan Kalor: Radiasi
Berbeda dengan proses konduksi dan konveksi yang membutuhkan zat perantara, perambatan kalor melalui proses radiasi tidak melalui zat perantara. Contoh yang paling sederhana adalah proses merambatnya kalor dari matahari sampai ke permukaan bumi. Kalor merambat melalui ruang hampa sebelum mencapai atmosfer bumi. Hal ini disebabkan oleh karakteristik dasar radiasi yang sebenarnya berupa gelombang elektromagnet. Jadi dalam radiasi matahari, terdapat seluruh spektrum elektromagnet yang tidak perlu medium untuk merambat. Laju aliran kalor melalui radiasi sebanding dengan luas penampang $\left( A \right)$yang memancarkan radiasi. Jika ada benda bersuhu $T$ memancarkan radiasi kalor, maka besar laju rambatan kalornya adalah:
$\frac{Q}{t}=e\ \sigma \ A\ {{T}^{4}}\quad \ldots \ldots \ldots \ldots \ldots \left( 8 \right)$
Pada persamaan 8 di atas, $e$ adalah emisivitas bahan atau kemampuan memancarkan radiasi, dengan nilai $0<e<1$. Jika semakin hitam permukaan benda, maka emisivitasnya semakin mendekati nilai 1. Karena warna hitam juga penyerap kalor yang baik, maka dapat dikatakan bahwa penyerap kalor yang baik juga merupakan pemancar kalor yang baik. Sedangkan nilai $\sigma =5,67\times {{10}^{-8}}\ {W}/{{{m}^{2}}\cdot {{K}^{4}}}\;$ yang merupakan konstanta Stefan-Boltzmann.
Sebuah benda dapat menyerap radiasi sekaligus memancarkan radiasi. Untuk laju penyerapan kalor juga berlaku persamaan 8 di atas. Jika dihitung laju aliran kalor total suatu benda akibat radiasi, dapat digunakan persamaan berikut:
${{\left( \frac{Q}{t} \right)}_{total}}={{\left( \frac{Q}{t} \right)}_{serap}}-\quad {{\left( \frac{Q}{t} \right)}_{emisi}} \\ $
${{\left( \frac{Q}{t} \right)}_{total}}=e\ \sigma \ A\ \left[ {{\left( {{T}_{serap}} \right)}^{4}}-{{\left( {{T}_{emisi}} \right)}^{4}} \right] \\ $
Contoh Soal Perpindahan Kalor Radiasi:
Seorang petinju sedang duduk di dalam ruang ganti tepat setelah bertanding. Cat tembok ruang ganti memiliki warna yang gelap. Jika suhu kulit petinju adalah $34{{\ }^{o}}C$ dan suhu permukaan tembok adalah $15{{\ }^{o}}C$, maka perkiraan laju radiasi kalor yang dilepas oleh tubuh petinju adalah...
(asumsikan luas permukaan tubuh petinju adalah $1,5\ {{m}^{2}}$ dengan $e=0,7$).
Jawab:
Perlu diingat bahwa suhu harus dalam satuan Kelvin.
${{\left( \frac{Q}{t} \right)}_{total}}=e\ \sigma \ A\ \left[ {{\left( {{T}_{serap}} \right)}^{4}}-{{\left( {{T}_{emisi}} \right)}^{4}} \right] \\$
${{\left( \frac{Q}{t} \right)}_{total}}=0,7\cdot \ \left( 5,67\times {{10}^{-8}} \right)\cdot 1,5\ \left[ {{\left( 307 \right)}^{4}}-{{\left( 288 \right)}^{4}} \right] \\$
${{\left( \frac{Q}{t} \right)}_{total}}\approx 120\ Watt \\ $