Konsep dan Contoh Soal Hukum Kirchhoff – Rangkaian Loop - Fisika SMA Kelas 12
Jul 12, 2019
Edit
a. Aturan percabangan jalur rangkaian (junction rule), menyatakan bahwa jumlah kuat arus listrik yang masuk percabangan harus sama dengan jumlah arus listrik yang meninggalkan percabangan.
b. Aturan Loop (Loop Rule), menyatakan bahwa jumlah beda potensial dalam rangkaian tertutup harus sama dengan nol.
1. Konsep Hukum Kirchoff 1 (tentang arus listrik)
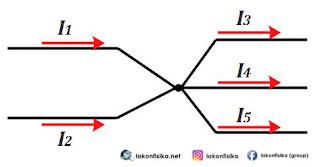
Hukum Kirchoff 1 merupakan pernyataan tentang hukum kekekalan muatan listrik. Jumlah muatan listrik yang masuk dan keluar titik percabangan jalur rangkaian harus sama konstan. Karena aliran muatan listrik disebut sebagai arus listrik, maka Hukum Kirchoff 2 bisa dinyatakan sebagai hukum kekekalan arus listrik. Ilustrasi arus listrik di titik percabangan dapat dilihat pada Gambar di bawah.
 |
| Ilustrasi Arus yang Masuk dan Keluar Titik Percabangan |
Berdasarkan ilustrasi di atas, kuat arus listrik yang masuk percabangan harus sama dengan jumlah kuat arus listrik yang keluar percabangan. Hukum Kirchoff 1 dapat dinyatakan secara matematis dalam persamaan 1 di bawah ini.
$\sum{{{I}_{masuk}}}=\sum{{{I}_{keluar}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
Berdasarkan persamaan 1, Hukum Kirchoff 1 dapat diuraikan menjadi:
${{I}_{1}}+{{I}_{2}}={{I}_{3}}+{{I}_{4}}+{{I}_{5}}$
2. Konsep Hukum Kirchoff 2 (tentang beda potensial)
Hukum Kirchoff 2 merupakan implementasi hukum kekekalan energi pada rangkaian listrik tertutup. Jadi ketika muatan yang mengalir dalam rangkaian sudah kembali ke titik awal, jumlah energinya harus sama dengan sebelum muatan tersebut bergerak. Hal ini akan berkaitan dengan transisi energi ketika muatan melewati resistor dan melewati sumber tegangan. Energi dalam rangkaian listrik bersumber dari potensial listrik di setiap titiknya, dan karena bersifat kekal, maka jumlah beda potensial dalam rangkaian tertutup harus nol. Jadi secara sederhana, Hukum Kirchoff 2 dapat dinyatakan dalam persamaan 2 berikut ini.
$\sum{\Delta V}=0$ , karena beda potensial terjadi pada resistor dan sumber tegangan, maka persamaan tersebut dapat dinyatakan dengan:
$\sum{V}+\sum{\left( I\cdot R \right)}=0\quad \ldots \ldots \ldots \ldots \ldots \left( 2 \right)$
 |
| Ilustrasi Loop Arus Listrik dalam Rangkaian Tertutup |
Untuk menganalisis rangkaian dengan Hukum Kirchoff, yang perlu dilakukan adalah membuat loop arus listrik (permisalan perputaran arus listrik), seperti ilustrasi gambar di atas. Panah merah yang melingkar menunjukkan arah putaran loop, yang merupakan permisalan arah putaran arus listrik.
Selanjutnya kita bayangkan berjalan dalam rangkaian dengan mengikuti arah loop sambil mengisi besaran-besaran di persamaan 2, caranya sebagai berikut:
a. Misalkan kita mulai berjalan dari titik a dan harus kembali ke titik a lagi. Jika arah loop ke kanan seperti gambar di atas, maka kita berputar ke kanan sesuai loop. Yang perlu diisi adalah $\sum{V}$ dan $\sum{\left( I\cdot R \right)}$.
b. Cara mengisi $\sum{V}$: Jika dalam perjalanan ketemu kutub negatif sumber tegangan $\left( V \right)$, maka kita tuliskan tanda negatif. Jika ketemu kutub positif sumber tegangan, maka dituliskan tanda positif.
c. Cara mengisi $\sum{\left( I\cdot R \right)}$: Jika ada satu loop berarti arus listrik $\left( I \right)$ yang melewati sama, tinggal dituliskan jumlah arus listrik dikalikan masing-masing hambatan yang dilewati selama perjalanan.
Sesuai cara di atas, rumusan Hukum kirchoff 2 pada ilustrasi rangkaian dapat dinyatakan sebagai berikut ini:
$\left( -{{V}_{2}}-{{V}_{1}} \right)+\left( I\cdot {{R}_{1}}+I\cdot {{R}_{2}}+I\cdot {{R}_{3}} \right)=0$
$-{{V}_{2}}-V+I\left( {{R}_{1}}+{{R}_{2}}+{{R}_{3}} \right)=0$
Contoh Soal Hukum Kirchoff 1 Loop
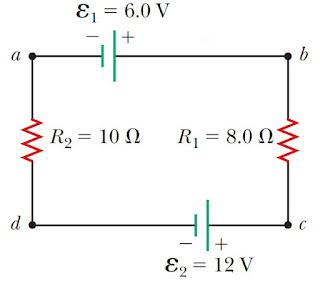
Suatu rangkaian tertutup memiliki 2 resistor dan 2 sumber tegangan seperti gambar di bawah. Asumsikan tidak ada hambatan dalam baterai. Tentukan kuat arus listrik yang mengalir dalam rangkaian tersebut!
Jawab:
Yang pertama kita lakukan adalah membuat arah loop dalam rangkaian seperti gambar berikut ini.
Selanjutnya, kita mulai perjalanan dari titik a ke kanan mengikuti arah loop sampai berakhir di titik a lagi, sambil mengisi persamaan Hukum Kirchoff 2.
Yang pertama kita lakukan adalah membuat arah loop dalam rangkaian seperti gambar berikut ini.
Selanjutnya, kita mulai perjalanan dari titik a ke kanan mengikuti arah loop sampai berakhir di titik a lagi, sambil mengisi persamaan Hukum Kirchoff 2.
$\left( -{{\varepsilon }_{1}}+{{\varepsilon }_{2}} \right)+I\left( {{R}_{1}}+{{R}_{2}} \right)=0$
$-6+12+I\left( 8+10 \right)=0$
$6+18I=0$
$I=-\frac{1}{3}\ Ampere$
Berdasarkan hasil perhitungan, nilai kuat arus listrik adalah $\frac{1}{3}A$. Tanda negatif pada nilai arus listrik hanya menunjukkan bahwa permisalan loop arus listrik terbalik, artinya arus listrik sebenarnya memiliki arah putaran loop ke kiri, bukan ke kanan.
Contoh Soal Hukum Kirchoff 2 Loop
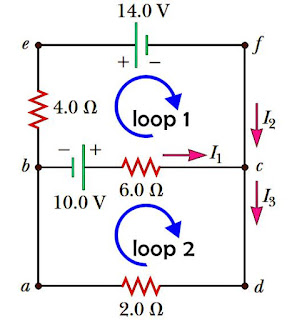
(1). Tentukan besar kuat arus listrik ${{I}_{1}}$, ${{I}_{2}}$, dan ${{I}_{3}}$ pada rangkaian di bawah ini!
Jawab:
Pada soal ini, rangkaian harus dibuat menjadi 2 loop, yang ditandai dengan adanya 2 sumber tegangan dengan jalur yang berbeda (tidak satu jalur). Jika ada lebih dari satu sumber tegangan yang berbeda jalur arus listrik, maka harus dibuat lebih dari 1 loop, bisa 2 atau lebih, tergantung model rangkaian.
Gambar rangkaian pada soal ini juga sudah menunjukkan masing-masing arus listrik, jadi kita tinggal mengikuti arahnya, dengan membuat 2 loop seperti gambar di bawah. Teknik mengerjakan soal lebih dari satu loop ini sebenarnya dengan sistem persamaan linier. Karena pada soal sudah ditentukan ada 3 arus listrik, maka nanti akan ada 3 persamaan linier 3 variabel yaitu ${{I}_{1}}$, ${{I}_{2}}$, dan ${{I}_{3}}$.
Berdasarkan Hukum Kirchoff 1, di titik c berlaku persamaan berikut ini:
Pada soal ini, rangkaian harus dibuat menjadi 2 loop, yang ditandai dengan adanya 2 sumber tegangan dengan jalur yang berbeda (tidak satu jalur). Jika ada lebih dari satu sumber tegangan yang berbeda jalur arus listrik, maka harus dibuat lebih dari 1 loop, bisa 2 atau lebih, tergantung model rangkaian.
Gambar rangkaian pada soal ini juga sudah menunjukkan masing-masing arus listrik, jadi kita tinggal mengikuti arahnya, dengan membuat 2 loop seperti gambar di bawah. Teknik mengerjakan soal lebih dari satu loop ini sebenarnya dengan sistem persamaan linier. Karena pada soal sudah ditentukan ada 3 arus listrik, maka nanti akan ada 3 persamaan linier 3 variabel yaitu ${{I}_{1}}$, ${{I}_{2}}$, dan ${{I}_{3}}$.
Berdasarkan Hukum Kirchoff 1, di titik c berlaku persamaan berikut ini:
Hasil analisis loop 1, berjalan melewati urutan titik $befcb$:
$\begin{align} & \sum{V}+\sum{\left( I\cdot R \right)}=0 \\ & 14+10+{{I}_{2}}\left( 4 \right)-{{I}_{1}}\left( 6 \right)=0 \\ & \quad \quad \quad \left( {{I}_{1}}\text{ bertanda (-) karena berlawanan dengan arah loop1} \right) \\ & -6\ {{I}_{1}}+4\ {{I}_{2}}=-24\quad \ldots \ldots \ldots \ldots \ldots \left( b \right) \\ \end{align}$
Hasil analisis loop 2, berjalan melewati urutan titik $abcda$:
$\begin{align} & \sum{V}+\sum{\left( I\cdot R \right)}=0 \\ & -10+{{I}_{1}}\left( 6 \right)+{{I}_{3}}\left( 2 \right)=0 \\ & 6\ {{I}_{1}}+2\ {{I}_{3}}=10\quad \ldots \ldots \ldots \ldots \ldots \left( c \right) \\ \end{align}$
Substitusikan nilai ${{I}_{3}}$ dari persamaan a ke persamaan c:
$\begin{align} & 6\ {{I}_{1}}+2\ \left( {{I}_{1}}+{{I}_{2}} \right)=10 \\ & 8\ {{I}_{1}}+2\ {{I}_{2}}=10\quad \ldots \ldots \ldots \ldots \ldots \left( d \right) \\ \end{align}$
Tentukan solusi persamaan b dan d melalui teknik eliminasi dan substitusi untuk mendapatkan nilai ${{I}_{1}}$ dan ${{I}_{2}}$.
$\begin{align} & -6\ {{I}_{1}}+4\ {{I}_{2}}=-24\left. {} \right|\times 1\left| \text{ }-6\ {{I}_{1}}+4\ {{I}_{2}}=-24 \right. \\ & 8\ {{I}_{1}}+2\ {{I}_{2}}=10\left. \text{ } \right|\times 2\left| \text{ 16}\ {{I}_{1}}+4\ {{I}_{2}}=20 \right. \end{align}$
Hasil pengurangannya adalah:
$\begin{align} & -22\ {{I}_{1}}=-44 \\ & {{I}_{1}}=\frac{44}{22}=2\ A \\ \end{align}$
Kita substitusikan nilai ${{I}_{1}}$ ke persamaan d untuk mendapatkan nilai ${{I}_{2}}$.
$\begin{align} & 8\ \left( 2 \right)+2\ {{I}_{2}}=10 \\ & 2\ {{I}_{2}}=10-16 \\ & 2\ {{I}_{2}}=-6 \\ & {{I}_{2}}=-3\ A \\ \end{align}$
Selanjutnya kita hitung ${{I}_{3}}$ dengan persamaan a.
$\begin{align} & {{I}_{1}}+{{I}_{2}}={{I}_{3}} \\ & {{I}_{3}}=2+\left( -3 \right) \\ & {{I}_{3}}=-1\ A \\ \end{align}$
Jadi masing-masing nilai ${{I}_{1}}=2\ A$; ${{I}_{2}}=-3\ A$ (arah berkebalikan dengan gambar), dan ${{I}_{3}}=-1\ A$ (arah berkebalikan dengan gambar).
$\begin{align} & \sum{V}+\sum{\left( I\cdot R \right)}=0 \\ & 14+10+{{I}_{2}}\left( 4 \right)-{{I}_{1}}\left( 6 \right)=0 \\ & \quad \quad \quad \left( {{I}_{1}}\text{ bertanda (-) karena berlawanan dengan arah loop1} \right) \\ & -6\ {{I}_{1}}+4\ {{I}_{2}}=-24\quad \ldots \ldots \ldots \ldots \ldots \left( b \right) \\ \end{align}$
Hasil analisis loop 2, berjalan melewati urutan titik $abcda$:
$\begin{align} & \sum{V}+\sum{\left( I\cdot R \right)}=0 \\ & -10+{{I}_{1}}\left( 6 \right)+{{I}_{3}}\left( 2 \right)=0 \\ & 6\ {{I}_{1}}+2\ {{I}_{3}}=10\quad \ldots \ldots \ldots \ldots \ldots \left( c \right) \\ \end{align}$
Substitusikan nilai ${{I}_{3}}$ dari persamaan a ke persamaan c:
$\begin{align} & 6\ {{I}_{1}}+2\ \left( {{I}_{1}}+{{I}_{2}} \right)=10 \\ & 8\ {{I}_{1}}+2\ {{I}_{2}}=10\quad \ldots \ldots \ldots \ldots \ldots \left( d \right) \\ \end{align}$
Tentukan solusi persamaan b dan d melalui teknik eliminasi dan substitusi untuk mendapatkan nilai ${{I}_{1}}$ dan ${{I}_{2}}$.
$\begin{align} & -6\ {{I}_{1}}+4\ {{I}_{2}}=-24\left. {} \right|\times 1\left| \text{ }-6\ {{I}_{1}}+4\ {{I}_{2}}=-24 \right. \\ & 8\ {{I}_{1}}+2\ {{I}_{2}}=10\left. \text{ } \right|\times 2\left| \text{ 16}\ {{I}_{1}}+4\ {{I}_{2}}=20 \right. \end{align}$
Hasil pengurangannya adalah:
$\begin{align} & -22\ {{I}_{1}}=-44 \\ & {{I}_{1}}=\frac{44}{22}=2\ A \\ \end{align}$
Kita substitusikan nilai ${{I}_{1}}$ ke persamaan d untuk mendapatkan nilai ${{I}_{2}}$.
$\begin{align} & 8\ \left( 2 \right)+2\ {{I}_{2}}=10 \\ & 2\ {{I}_{2}}=10-16 \\ & 2\ {{I}_{2}}=-6 \\ & {{I}_{2}}=-3\ A \\ \end{align}$
Selanjutnya kita hitung ${{I}_{3}}$ dengan persamaan a.
$\begin{align} & {{I}_{1}}+{{I}_{2}}={{I}_{3}} \\ & {{I}_{3}}=2+\left( -3 \right) \\ & {{I}_{3}}=-1\ A \\ \end{align}$
Jadi masing-masing nilai ${{I}_{1}}=2\ A$; ${{I}_{2}}=-3\ A$ (arah berkebalikan dengan gambar), dan ${{I}_{3}}=-1\ A$ (arah berkebalikan dengan gambar).
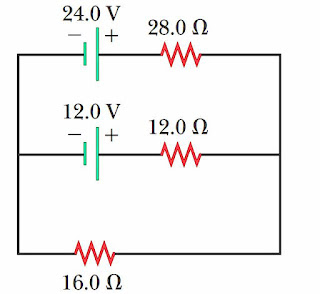
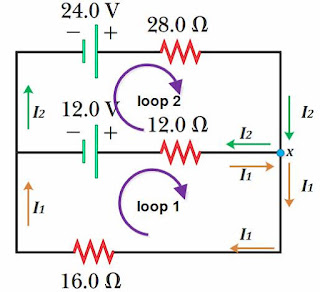
(2). Tentukan besar disipasi daya pada hambatan $12\ \Omega $ dari rangkaian di bawah ini!
Jawab:
Langkah pertama yang dilakukan adalah membuat loop pada rangkaian seperti gambar di bawah. Hasilnya, ada dua arus listrik yang didefinisikan pada titik percabangan x, yaitu ${{I}_{1}}$ dan ${{I}_{2}}$.
Selanjutnya kita analisis masing-masing loop. Kita asumsikan hanya ada 2 arus listrik saja, jadi di jalur tengah mengalir arus listrik ${{I}_{1}}$ dan ${{I}_{2}}$ yang saling berlawanan arah.
Analisis loop 1, loop berputar ke kanan dan di jalur tengah ada arus ${{I}_{2}}$ yang berlawanan arah loop.
$\begin{align} & \sum{V}+\sum{\left( I\cdot R \right)}=0 \\ & -12+{{I}_{1}}\left( 12 \right)-{{I}_{2}}\left( 12 \right)+{{I}_{1}}\left( 16 \right)=0 \\ & 28\ {{I}_{1}}-12\ {{I}_{2}}=12 \\ & 7\ {{I}_{1}}-3\ {{I}_{2}}=3\quad \ldots \ldots \ldots \ldots \ldots \left( a \right) \\ \end{align}$
Analisis loop 2, loop berputar ke kanan dan di jalur tengah ada arus ${{I}_{1}}$ yang berlawanan arah loop.
$\begin{align} & \sum{V}+\sum{\left( I\cdot R \right)}=0 \\ & -24+12+{{I}_{2}}\left( 28 \right)+{{I}_{2}}\left( 12 \right)-{{I}_{1}}\left( 12 \right)=0 \\ & -12\ {{I}_{1}}+40\ {{I}_{2}}=12 \\ & 3\ {{I}_{1}}-10\ {{I}_{2}}=-3\quad \ldots \ldots \ldots \ldots \ldots \left( b \right) \\ \end{align}$
Kemudian kita tentukan solusi persamaan a dan b dengan teknik eliminasi dan substitusi untuk mendapatkan nilai ${{I}_{1}}$ dan ${{I}_{2}}$.
$\begin{align} & 7\ {{I}_{1}}-3\ {{I}_{2}}=\ \ \ 3\left. {} \right|\times 10\left| \text{ }70\ {{I}_{1}}-30\ {{I}_{2}}=30 \right. \\ & 3\ {{I}_{1}}-10\ {{I}_{2}}=-3\left. {} \right|\times 3\ \ \left| \text{ }\ \ 9\ {{I}_{1}}-30\ {{I}_{2}}=-9 \right. \end{align}$
Hasil pengurangannya adalah:
$\begin{align} & 61\ {{I}_{1}}=39 \\ & {{I}_{1}}=\frac{39}{61}\approx 0,64\ A \\ \end{align}$
Substitusikan nilai ${{I}_{1}}$ ke persamaan b:
$\begin{align} & 3\ \left( \frac{39}{61} \right)-10\ {{I}_{2}}=-3 \\ & -10\ {{I}_{2}}=-3-\frac{108}{61} \\ & -10\ {{I}_{2}}=\frac{-183-108}{61} \\ & -10\ {{I}_{2}}=\frac{-291}{61} \\ & {{I}_{2}}=\frac{291}{610}\approx 0,48\ A \\ \end{align}$
Untuk menentukan daya pada hambatan $12\ \Omega $, kita perlu cari nilai arus pada hambatan tersebut, kita misalkan di percabangan x adalah titik temu 3 arus listrik sesuai Hukum Kirchoff 1.
$\begin{align} & {{I}_{3}}={{I}_{1}}-{{I}_{2}} \\ & {{I}_{3}}=0,64-0,48 \\ & {{I}_{3}}=0,16\ A \\ \end{align}$
Sekarang kita hitung disipasi daya pada hambatan $12\ \Omega $.
$\begin{align} & {{P}_{12}}={{\left( {{I}_{3}} \right)}^{2}}\cdot 12 \\ & {{P}_{12}}={{\left( 0,16 \right)}^{2}}\cdot 12 \\ & {{P}_{12}}\approx 0,31\ watt \\ \end{align}$
Jadi besar disipasi daya pada hambatan $12\ \Omega $ adalah 0,31 watt.
Langkah pertama yang dilakukan adalah membuat loop pada rangkaian seperti gambar di bawah. Hasilnya, ada dua arus listrik yang didefinisikan pada titik percabangan x, yaitu ${{I}_{1}}$ dan ${{I}_{2}}$.
Selanjutnya kita analisis masing-masing loop. Kita asumsikan hanya ada 2 arus listrik saja, jadi di jalur tengah mengalir arus listrik ${{I}_{1}}$ dan ${{I}_{2}}$ yang saling berlawanan arah.
Analisis loop 1, loop berputar ke kanan dan di jalur tengah ada arus ${{I}_{2}}$ yang berlawanan arah loop.
Analisis loop 2, loop berputar ke kanan dan di jalur tengah ada arus ${{I}_{1}}$ yang berlawanan arah loop.
$\begin{align} & \sum{V}+\sum{\left( I\cdot R \right)}=0 \\ & -24+12+{{I}_{2}}\left( 28 \right)+{{I}_{2}}\left( 12 \right)-{{I}_{1}}\left( 12 \right)=0 \\ & -12\ {{I}_{1}}+40\ {{I}_{2}}=12 \\ & 3\ {{I}_{1}}-10\ {{I}_{2}}=-3\quad \ldots \ldots \ldots \ldots \ldots \left( b \right) \\ \end{align}$
Kemudian kita tentukan solusi persamaan a dan b dengan teknik eliminasi dan substitusi untuk mendapatkan nilai ${{I}_{1}}$ dan ${{I}_{2}}$.
$\begin{align} & 7\ {{I}_{1}}-3\ {{I}_{2}}=\ \ \ 3\left. {} \right|\times 10\left| \text{ }70\ {{I}_{1}}-30\ {{I}_{2}}=30 \right. \\ & 3\ {{I}_{1}}-10\ {{I}_{2}}=-3\left. {} \right|\times 3\ \ \left| \text{ }\ \ 9\ {{I}_{1}}-30\ {{I}_{2}}=-9 \right. \end{align}$
Hasil pengurangannya adalah:
$\begin{align} & 61\ {{I}_{1}}=39 \\ & {{I}_{1}}=\frac{39}{61}\approx 0,64\ A \\ \end{align}$
Substitusikan nilai ${{I}_{1}}$ ke persamaan b:
$\begin{align} & 3\ \left( \frac{39}{61} \right)-10\ {{I}_{2}}=-3 \\ & -10\ {{I}_{2}}=-3-\frac{108}{61} \\ & -10\ {{I}_{2}}=\frac{-183-108}{61} \\ & -10\ {{I}_{2}}=\frac{-291}{61} \\ & {{I}_{2}}=\frac{291}{610}\approx 0,48\ A \\ \end{align}$
Untuk menentukan daya pada hambatan $12\ \Omega $, kita perlu cari nilai arus pada hambatan tersebut, kita misalkan di percabangan x adalah titik temu 3 arus listrik sesuai Hukum Kirchoff 1.
$\begin{align} & {{I}_{3}}={{I}_{1}}-{{I}_{2}} \\ & {{I}_{3}}=0,64-0,48 \\ & {{I}_{3}}=0,16\ A \\ \end{align}$
Sekarang kita hitung disipasi daya pada hambatan $12\ \Omega $.
$\begin{align} & {{P}_{12}}={{\left( {{I}_{3}} \right)}^{2}}\cdot 12 \\ & {{P}_{12}}={{\left( 0,16 \right)}^{2}}\cdot 12 \\ & {{P}_{12}}\approx 0,31\ watt \\ \end{align}$
Jadi besar disipasi daya pada hambatan $12\ \Omega $ adalah 0,31 watt.