Konsep dan Contoh Soal Hukum Coulomb – Gaya Coulomb - Fisika SMA Kelas 12
Jul 15, 2019
Edit
Pada materi fisika SMA kelas 12, fenomena elektrostatik (listrik statis) akan dibahas lebih mendalam. Pembahasan konsep listrik statis lebih fokus pada interaksi antar muatan listrik berdasarkan sifat kelistrikan masing-masing muatan. Beberapa topik yang akan dibahas pada materi fisika SMA kelas 12 terkait listrik statis adalah:
a. Hukum Coulomb, yang membahas gaya interaksi antar muatan listrik yaitu gaya Coulomb atau gaya elektrostatik.
b. Medan listrik dari sebuah muatan dan pengaruh medan listrik dari beberapa muatan.
c. Potensial listrik dan energi potensial listrik
Kita akan fokus mempelajari konsep Hukum Coulomb dan contoh soal Hukum Coulomb dalam artikel ini.
Hukum Coulomb (Gaya Coulomb)
Ada 2 jenis muatan listrik, yaitu muatan positif dan muatan negatif. Muatan listrik dapat saling berinteraksi satu sama lain. Interaksi antar muatan listrik dapat berupa tarikan atau dorongan satu sama lain yang disebut sebagai gaya Coulomb atau gaya elektrostatik. Antara 2 muatan sejenis dapat menghasilkan gaya tolakan satu sama lain. Sedangkan antar muatan berbeda jenis menghasilkan gaya tolakan satu sama lain. Ilustrasinya dapat dilihat pada gambar di bawah ini.
 |
| Gaya Coulomb Antar Dua Muatan Listrik |
Masing-masing gambar a, b, dan c menunjukkan interaksi antara 2 muatan. Pada gambar a, dua muatan positif menghasilkan gaya tolak pada masing-masing ${{q}_{1}}$ dan ${{q}_{2}}$. Muatan ${{q}_{1}}$ mendapat gaya tolakan ${{F}_{12}}$ ke kiri akibat interaksi dengan muatan ${{q}_{2}}$. Sedangkan muatan ${{q}_{2}}$ mendapat gaya tolakan ${{F}_{21}}$ ke kanan akibat interaksi dengan muatan ${{q}_{1}}$. Begitu pun terjadi pada gambar b yang merupakan interaksi dua muatan negatif, terjadi gaya tolakan pada masing-masing muatan ${{q}_{1}}$ dan ${{q}_{2}}$. Sedangkan pada gambar c, terjadi interaksi antar dua muatan yang berbeda jenis, positif dan negatif, terjadi gaya saling tarik. Muatan ${{q}_{1}}$ ditarik muatan ${{q}_{2}}$ dengan gaya ${{F}_{12}}$ ke kanan, sedangkan muatan ${{q}_{2}}$ ditarik oleh muatan ${{q}_{1}}$ dengan gaya ${{F}_{21}}$ ke kiri. Perlu diperhatikan, konsep tersebut harus dipahami karena sangat penting digunakan untuk menentukan interaksi lebih dari dua muatan.
Berdasarkan Hukum Coulomb, besar gaya interaksi antar dua muatan memiliki besar yang sama pada masing-masing muatan $\left( {{F}_{12}}={{F}_{21}} \right)$. Besar gaya Coulomb tersebut dipengaruhi suatu konstanta $\left( k=\frac{1}{4\,\pi \,\varepsilon } \right)$, dengan nilai yang dipengaruhi oleh permitivitas medium $\left( \varepsilon \right)$. Jika muatan berada dalam medium udara, maka nilai $k\approx \ \,9\times {{10}^{9}}N\cdot {{{m}^{2}}}/{{{C}^{2}}}\;$. Besar gaya Coulomb antara dua muatan listrik dapat ditentukan dengan persamaan 1 berikut ini.
${{F}_{12}}={{F}_{21}}=F=k\frac{{{q}_{1}}\,{{q}_{2}}}{{{r}^{2}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
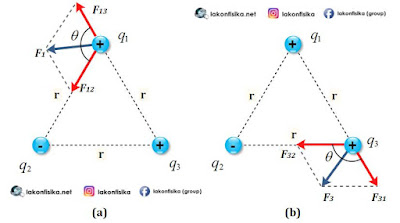
Gaya Coulomb merupakan besaran vektor, jadi untuk melakukan analisis kita harus menerapkan kaidah-kaidah besaran vektor. Gambar di bawah ini menunjukkan interaksi antara tiga muatan listrik. Masing-masing ${{q}_{1}}$ bermuatan positif, ${{q}_{2}}$ bermuatan negatif, dan ${{q}_{3}}$ bermuatan positif menempati posisi membentuk segitiga sama sisi.
 |
| Gaya Coulomb Tiga Muatan Posisi Segitiga |
Jika kita diminta menentukan gaya Coulomb yang terjadi pada muatan ${{q}_{1}}$, maka perlu dilakukan analisis vektor gaya seperti gambar a. Muatan ${{q}_{1}}$ mendapat gaya tarikan menuju muatan ${{q}_{2}}$ sebesar ${{F}_{12}}$. Muatan ${{q}_{1}}$ juga mendapatkan gaya tolakan menjauhi ${{q}_{3}}$ sebesar ${{F}_{13}}$. Selanjutnya, gaya Coulomb pada muatan ${{q}_{1}}$ yaitu ${{F}_{1}}$, merupakan resultan dari gaya ${{F}_{12}}$ dan ${{F}_{13}}$. Besar resultan gaya Coulomb ${{F}_{1}}$ dapat ditentukan dengan persamaan resultan vektor seperti persamaan 2 berikut ini.
${{F}_{1}}=\sqrt{{{\left( {{F}_{13}} \right)}^{2}}+{{\left( {{F}_{12}} \right)}^{2}}+2\cdot {{F}_{13}}\cdot {{F}_{12}}\cdot \cos \theta }\quad \ldots \ldots \ldots \ldots \ldots \left( 2 \right)$
Bagaimana jika kita diminta menentukan gaya Coulomb yang terjadi di muatan ${{q}_{3}}$? Ilustrasinya bisa dilihat pada gambar b di atas. Cara analisisnya sama seperti ketika menentukan gaya Coulomb pada muatan ${{q}_{1}}$. Ingat ya, perlu diperhatikan jenis muatan yang berinteraksi, karena akan menentukan arah gaya Coulombnya.
Contoh Soal Hukum Coulomb (Gaya Coulomb)
(1). Jika dua muatan ${{q}_{1}}$ dan ${{q}_{2}}$ terpisah sejauh $d$, maka masing-masing muatan akan mengalami gaya Coulomb sebesar $F$. Jika muatan ${{q}_{2}}$ bergeser sejauh $\frac{1}{3}d$ mendekati ${{q}_{1}}$, maka besar gaya Coulomb adalah...
Jawab:
Untuk mengerjakan model soal dengan dua kondisi berbeda seperti ini, kita gunakan teknik perbandingan. Kita bandingkan kondisi 1 dan kondisi 2.
${{r}_{1}}=d\quad \to \quad {{r}_{2}}=d-\frac{1}{3}d=\frac{2}{3}d$
${{F}_{1}}=F\quad \to \quad {{F}_{2}}=?$
$\frac{{{F}_{2}}}{{{F}_{1}}}=\frac{k\frac{{{q}_{1}}\,{{q}_{2}}}{r_{2}^{2}}}{k\frac{{{q}_{1}}\,{{q}_{2}}}{r_{1}^{2}}}\quad \quad \left( k,\ \ {{q}_{1}},\ \,{{q}_{2}}\text{ dapat dieliminasi} \right)$
$\frac{{{F}_{2}}}{{{F}_{1}}}=\frac{{}^{1}/{}_{r_{2}^{2}}}{{}^{1}/{}_{r_{1}^{2}}}=\frac{r_{1}^{2}}{r_{2}^{2}}$
$\frac{{{F}_{2}}}{F}=\frac{{{\left( d \right)}^{2}}}{{{\left( \frac{2}{3}d \right)}^{2}}}$
$\frac{{{F}_{2}}}{F}=\frac{1}{\left( \frac{4}{9} \right)}=\frac{9}{4}$
${{F}_{2}}=\frac{9}{4}F$
Jadi besar gaya Coulomb setelah muatan ${{q}_{2}}$ bergeser sejauh $\frac{1}{3}d$ mendekati ${{q}_{1}}$ adalah $\frac{9}{4}F$.
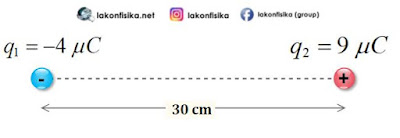
(2). Tiga partikel bermuatan listrik masing-masing berada dalam posisi satu garis lurus seperti gambar di bawah. Gaya Coulomb yang terjadi pada muatan ${{Q}_{3}}\left( 4\ \mu C \right)$
akibat interaksi dengan muatan ${{Q}_{1}}\left( 8\ \mu C \right)$ dan ${{Q}_{2}}\left( -3\ \mu C \right)$ adalah...
Jawab:
Kita tentukan dulu masing-masing gaya Coulomb di ${{Q}_{3}}$ akibat pengaruh muatan ${{Q}_{1}}$ $\left( {{F}_{31}} \right)$ dan akibat pengaruh muatan ${{Q}_{2}}$ $\left( {{F}_{32}} \right)$ dengan arah seperti gambar di bawah ini.
Jangan lupa, masing-masing satuan muatan harus di rubah dalam Sistem Internasional $\left( 1\ \mu C={{10}^{-6}}C \right)$.
${{F}_{31}}=k\frac{{{Q}_{3}}\,{{Q}_{1}}}{{{\left( {{r}_{13}} \right)}^{2}}}$
${{F}_{31}}=9\times {{10}^{9}}\frac{\left( 4\times {{10}^{-6}} \right)\,\left( 8\times {{10}^{-6}} \right)}{{{\left( 5\times {{10}^{-1}} \right)}^{2}}}$
${{F}_{31}}\approx 1,2\ N$
${{F}_{32}}=k\frac{{{Q}_{3}}\,{{Q}_{2}}}{{{\left( {{r}_{23}} \right)}^{2}}}$
${{F}_{32}}=9\times {{10}^{9}}\frac{\left( 4\times {{10}^{-6}} \right)\,\left( 3\times {{10}^{-6}} \right)}{{{\left( 2\times {{10}^{-1}} \right)}^{2}}}$
${{F}_{32}}=2,7\ N$
Karena masing-masing gaya ${{F}_{31}}$ dan ${{F}_{32}}$ berada dalam satu sumbu (segaris), maka untuk mencari resultan cukup kita gunakan prinsip penjumlahan dengan arah ke kanan kita beri tanda (+) dan arah ke kiri bertanda (-).
${{F}_{3}}=-{{F}_{32}}+{{F}_{31}}$
${{F}_{3}}=-2,7+1,2$
${{F}_{3}}=-1,5\ N$
Jadi besar gaya Coulomb pada muatan ${{Q}_{3}}$ adalah sebesar $1,5\ N$ dengan arah ke kiri (karena bertanda negatif).
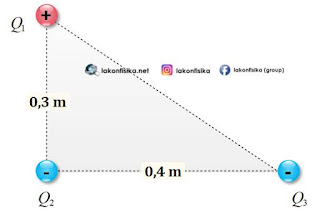
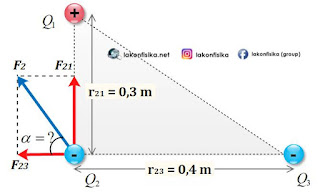
(3). Tiga partikel bermuatan listrik masing-masing ${{Q}_{1}}\left( 8\ \mu C \right)$, ${{Q}_{2}}\left( -3\ \mu C \right)$, dan ${{Q}_{3}}\left( -4\ \mu C \right)$ berada dalam posisi seperti gambar di bawah. Gaya Coulomb yang terjadi pada muatan ${{Q}_{2}}$ adalah...
Jawab:
Langkah pertama yang harus dilakukan adalah menggambarkan sketsa masing-masing vektor gaya pada muatan ${{Q}_{2}}$ akibat interaksi dengan muatan ${{Q}_{1}}$ dan ${{Q}_{3}}$. Muatan ${{Q}_{2}}$ ditarik oleh gaya ${{F}_{21}}$ menuju muatan ${{Q}_{1}}$ dan ditolak oleh gaya ${{F}_{23}}$ menjauhi muatan ${{Q}_{3}}$.
Selanjutnya kita hitung masing-masing ${{F}_{21}}$ dan ${{F}_{23}}$. Jangan lupa, masing-masing satuan muatan harus di rubah dalam Sistem Internasional $\left( 1\ \mu C={{10}^{-6}}C \right)$.
${{F}_{21}}=k\frac{{{Q}_{2}}\,{{Q}_{1}}}{{{\left( {{r}_{21}} \right)}^{2}}}$
${{F}_{21}}=9\times {{10}^{9}}\frac{\left( 3\times {{10}^{-6}} \right)\,\left( 8\times {{10}^{-6}} \right)}{{{\left( 3\times {{10}^{-1}} \right)}^{2}}}$
${{F}_{21}}=2,4\ N$
${{F}_{23}}=k\frac{{{Q}_{2}}\,{{Q}_{3}}}{{{\left( {{r}_{23}} \right)}^{2}}}$
${{F}_{23}}=9\times {{10}^{9}}\frac{\left( 3\times {{10}^{-6}} \right)\,\left( 4\times {{10}^{-6}} \right)}{{{\left( 4\times {{10}^{-1}} \right)}^{2}}}$
${{F}_{23}}=6,75\ N$
Karena ${{F}_{21}}$ dan ${{F}_{23}}$ mengapit sudut ${{90}^{o}}$, maka resultan gaya $\left( {{F}_{2}} \right)$ bisa kita tentukan dengan prinsip Phytaghoras.
${{F}_{2}}=\sqrt{{{\left( {{F}_{21}} \right)}^{2}}+{{\left( {{F}_{23}} \right)}^{2}}}$
${{F}_{2}}=\sqrt{{{\left( 2,4 \right)}^{2}}+{{\left( 6,75 \right)}^{2}}}$
${{F}_{2}}\approx 7,2\ N$
Kemudian kita tentukan arah vektor resultan gaya ${{F}_{2}}$:
$\tan \alpha =\frac{{{F}_{21}}}{{{F}_{23}}}$
$\tan \alpha =\frac{2,4}{6,75}$
$\alpha ={{\tan }^{-1}}\left( \frac{2,4}{6,75} \right)$
$\alpha \approx 19,{{6}^{o}}$
Jadi gaya yang terjadi pada muatan ${{Q}_{2}}$ adalah sebesar ${{F}_{2}}\approx 7,2\ N$ dengan arah $\alpha \approx 19,{{6}^{o}}$terhadap sumbu x negatif seperti pada gambar di atas.
(4). Dua buah partikel bermuatan listrik masing-masing ${{q}_{1}}$ dan ${{q}_{2}}$. Kedua partikel terpisah dengan jarak $30\ cm$ seperti gambar di bawah. Jika ada muatan ${{q}_{3}}\left( 16\ \mu C \right)$ akan diletakkan di sekitar dua muatan tersebut, maka posisi ${{q}_{3}}$ agar resultan gaya Coulombnya nol adalah di...
Jawab:
Kita harus pahami bahwa resultan gaya bernilai nol jika ada dua gaya yang saling berlawanan arah dan sama besar. Untuk menentukan posisi muatan ${{q}_{3}}$, kita harus perkirakan masing-masing arah gaya Coulomb pada ${{q}_{3}}$ akibat interaksi dengan ${{q}_{1}}$ dan ${{q}_{2}}$. Masing-masing gaya tersebut harus saling berlawanan arah, ingat syarat resultan agar nilainya nol.
Kita bisa kategorikan menjadi 3 daerah seperti gambar di atas. Pada daerah 1, jika muatan ${{q}_{3}}$ diletakkan di sepanjang garis penghubung ${{q}_{1}}$ dan ${{q}_{2}}$ (garis putus-putus), maka dua gaya akan searah menuju ${{q}_{1}}$, jadi tidak mungkin resultan akan nol. Jika muatan ${{q}_{3}}$ diletakkan pada daerah 2 dan 3, maka masing-masing gaya akan berlawanan arah. Nah, selanjutnya, kita tinggal pilih daerah 2 dengan alasan besar gaya berbanding lurus dengan muatan, dan berbanding terbalik dengan kuadrat jarak. Karena ${{q}_{1}}<{{q}_{2}}$ dan ${{r}_{32}}>{{r}_{31}}$ , akan sangat mungkin nilai ${{F}_{32}}={{F}_{31}}$.
Dengan nilai ${{r}_{31}}=x\quad \text{dan}\quad {{r}_{32}}=\left( 30+x \right)$, selanjutnya kita analisis secara matematis melalui syarat resultan nol (kesetimbangan gaya).
${{F}_{32}}={{F}_{31}}$
$k\frac{{{q}_{3}}\ {{q}_{2}}}{{{\left( {{r}_{32}} \right)}^{2}}}=k\frac{{{q}_{3}}\ {{q}_{1}}}{{{\left( {{r}_{31}} \right)}^{2}}}$
$\frac{{{q}_{2}}}{{{\left( {{r}_{32}} \right)}^{2}}}=\frac{{{q}_{1}}}{{{\left( {{r}_{31}} \right)}^{2}}}$
$\frac{9}{{{\left( 30-x \right)}^{2}}}=\frac{4}{{{\left( x \right)}^{2}}}$ (nilai satuan tidak perlu dikonversi ke SI karena kita tinggal pakai prinsip perbandingan matematika)
$\sqrt{\frac{9}{{{\left( 30-x \right)}^{2}}}}=\sqrt{\frac{4}{{{\left( x \right)}^{2}}}}$ (dengan teknik matematis kita akar kedua ruas agar lebih sederhana)
$\frac{3}{30-x}=\frac{2}{x}$
$2\left( 30-x \right)=3x$
$60-2x=3x$
$5x=60$
$x=12\ cm$
Jadi posisi ${{q}_{3}}$ adalah 12 cm di sebelah kiri ${{q}_{1}}$.