Konsep dan Contoh Soal Fluida Dinamis – Hukum Bernoulli - Fisika SMA Kelas 11
Jul 2, 2019
Edit
Setelah belajar konsep fluida statis, sekarang kita akan belajar bersama tentang fluida dinamis (fluida yang bergerak/mengalir). Ada dua jenis utama aliran fluida, yaitu aliran laminer dan aliran turbulen. Pada aliran laminer, setiap partikel fluida mempunyai arah gerak relatif searah dan tidak saling bersilangan arah. Sedangkan aliran turbulen biasanya ditandai dengan adanya lingkaran-lingkaran kecil pada fluida atau seperti pusaran-pusaran.
Nah untuk melakukan analisis fluida yang riil, pasti banyak parameter yang diperhatikan, sehingga untuk Fisika SMA Kelas 11 hanya dipelajari materi fisika dasar dengan kondisi fluida ideal. Yang dimaksud fluida ideal ini adalah fluida yang diasumsikan memiliki karakteristik aliran stabil (steady flow), aliran yang tidak terkompresi (incompressible flow), aliran yang tidak kental (nonviscous flow), dan aliran yang tidak berotasi (irrotational flow). Pada materi Fisika SMA Kelas 11, konsep fluida dinamis memiliki dua topik bahasan utama yaitu konsep kontinuitas aliran (debit aliran) dan konsep Hukum Bernoulli. Selain itu, akan dibahas pula apikasi Hukum Bernoulli antara lain Teorema Torricelli tentang tabung bocor, semprotan nyamuk, sayap pesawat terbang, dan venturimeter. Soal pada topik-topik ini bisa saling dikombinasikan sehingga memenuhi karakteristik model soal HOTS fisika. Sekarang langsung saja kita pelajari bersama konsep dan contoh soal Fluida Dinamis dan Hukum Bernoulli pada materi Fisika SMA Kelas 11.
$\frac{\Delta {{m}_{1}}}{\Delta t}=\frac{\Delta {{m}_{2}}}{\Delta t}\ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
Pada gambar di atas, volume fluida yang melewati penampang 1 $\left( {{A}_{1}} \right)$ selama selang waktu $\left( \Delta t \right)$ adalah ${{A}_{1}}\ \Delta {{l}_{1}}$, dengan nilai $\Delta {{l}_{1}}$ adalah perpindahan massa fluida selama $\Delta t$. Fluida yang melewati ${{A}_{1}}$ memiliki massa jenis ${{\rho }_{1}}$ dengan kecepatan aliran fluida sebesar ${{v}_{1}}={}^{\Delta {{l}_{1}}}/{}_{\Delta t}$. Sehingga laju aliran massa fluida dapat diturunkan menjadi persamaan:
$\frac{\Delta {{m}_{1}}}{\Delta t}=\frac{{{\rho }_{1}}\ \Delta {{V}_{1}}}{\Delta t}=\frac{{{\rho }_{1}}\ {{A}_{1}}\ \Delta {{l}_{1}}}{\Delta t}={{\rho }_{1}}\ {{A}_{1}}\ {{v}_{1}}$
Dengan analisis yang sama, laju aliran massa pada penampang 2 adalah ${{\rho }_{2}}\ {{A}_{2}}\ {{v}_{2}}$, sehingga persamaan 1 tentang laju aliran massa fluida dapat dituliskan sebagai berikut:
$\begin{align}
& \frac{\Delta {{m}_{1}}}{\Delta t}=\frac{\Delta {{m}_{2}}}{\Delta t} \\
& {{\rho }_{1}}\ {{A}_{1}}\ {{v}_{1}}={{\rho }_{2}}\ {{A}_{2}}\ {{v}_{2}} \\
\end{align}$
Nah, di awal kita sudah batasi untuk jenis fluida ideal yang bersifat incompressible flow, artinya meskipun pipa berbeda penampang, massa jenis fluida $\rho $ tidak berubah atau konstan. Sehingga $\rho $ dapat dieliminasi. Sehingga dapat dinyatakan menjadi persamaan 2 berikut ini, yang disebut juga sebagai Persamaan Kontinuitas.
${{A}_{1}}\ {{v}_{1}}={{A}_{2}}\ {{v}_{2}}\ldots \ldots \ldots \ldots \ldots \left( 2 \right)$
Karena $v={}^{\Delta l}/{}_{\Delta t}$, maka persamaan 2 juga dapat dinyatakan sebagai laju volume fluida atau debit aliran fluida $\left( Q \right)$ yang konstan.
$\begin{align}
& {{A}_{1}}\ {{v}_{1}}={{A}_{2}}\ {{v}_{2}} \\
& {{A}_{1}}\ \frac{\Delta {{l}_{1}}}{\Delta t}={{A}_{2}}\ \frac{\Delta {{l}_{2}}}{\Delta t} \\
& \frac{\Delta {{V}_{1}}}{\Delta t}=\frac{\Delta {{V}_{2}}}{\Delta t} \\
& {{Q}_{1}}={{Q}_{2}} \\
\end{align}$
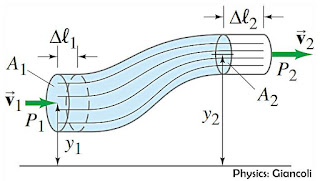
Pada gambar di atas, fluida memasuki ${{A}_{1}}$, kemudian mengalir sejauh $\Delta {{l}_{1}}$dan mendesak fluida pada ${{A}_{2}}$ untuk bergeser sejauh $\Delta {{l}_{2}}$. Fluida di sebelah kiri ${{A}_{1}}$ menekan fluida dalam luasan tersebut sebesar ${{p}_{1}}$ dan melakukan kerja sebesar:
${{W}_{1}}={{F}_{1}}\ \Delta {{l}_{1}}={{p}_{1}}\ {{A}_{1}}\ \Delta {{l}_{1}}\ldots \ldots \ldots \ldots \ldots $ dengan nilai $p=\frac{F}{A}$
Pada penampang 2, kerja yang dilakukan sebesar ${{W}_{2}}=-{{p}_{2}}\ {{A}_{2}}\ \Delta {{l}_{2}}$, tanda negatif disebabkan arah gaya berlawanan dengan arah perpindahan fluida. Selain itu, kerja juga dilakukan pada fluida oleh gaya gravitasi. Fluida mengalir dari ${{A}_{1}}$ menuju ${{A}_{2}}$ dan mengalami perpindahan posisi ketinggian dari ${{y}_{1}}$ menuju ${{y}_{2}}$ akibat kerja yang dilakukan gaya gravitasi $\left( {{W}_{3}} \right)$:
${{W}_{3}}=-m\,g\left( {{y}_{2}}-{{y}_{1}} \right)$
Selanjutnya total kerja yang terjadi pada fluida adalah:
$\begin{align}
& W={{W}_{1}}+{{W}_{2}}+{{W}_{3}} \\
& W={{p}_{1}}\ {{A}_{1}}\ \Delta {{l}_{1}}+\left( -{{p}_{2}}\ {{A}_{2}}\ \Delta {{l}_{2}} \right)+\left( -m\,g\left( {{y}_{2}}-{{y}_{1}} \right) \right) \\
\end{align}$
Karena kerja total sistem sama dengan perubahan energi kinetik, maka:
$\frac{1}{2}m\,v_{2}^{2}-\frac{1}{2}m\,v_{1}^{2}={{p}_{1}}\ {{A}_{1}}\ \Delta {{l}_{1}}-{{p}_{2}}\ {{A}_{2}}\ \Delta {{l}_{2}}-m\,g\,{{y}_{2}}+m\,g\,{{y}_{1}}$
Untuk fluida ideal (incompressible), nilai ${{A}_{1}}\ \Delta {{l}_{1}}={{A}_{2}}\ \Delta {{l}_{2}}=A\ \Delta l=V$(volume fluida). Persamaan di atas dapat dibagi dengan $V$ sehingga diperoleh:
$\begin{align}
& \frac{1}{2}\frac{m}{V}\,v_{2}^{2}-\frac{1}{2}\frac{m}{V}\,v_{1}^{2}={{p}_{1}}\ -{{p}_{2}}\ -\frac{m}{V}\,g\,{{y}_{2}}+\frac{m}{V}\,g\,{{y}_{1}} \\
& \frac{1}{2}\rho \,v_{2}^{2}-\frac{1}{2}\rho \,v_{1}^{2}={{p}_{1}}\ -{{p}_{2}}\ -\rho \,g\,{{y}_{2}}+\rho \,g\,{{y}_{1}} \\
\end{align}$
$ $
${{p}_{1}}+\frac{1}{2}\rho \,v_{1}^{2}+\rho \,g\,{{y}_{1}}=\ {{p}_{2}}\ +\frac{1}{2}\rho \,v_{2}^{2}+\rho \,g\,{{y}_{2}}\,\ldots \ldots \ldots \ldots \ldots \left( 3 \right)$
Persamaan 3 disebut sebagai Persamaan Bernoulli. Secara umum, hukum Bernoulli menyatakan bahwa jika kecepatan aliran fluida tinggi, maka tekanannya rendah dan jika kecepatan aliran fluida renda, maka tekanannya tinggi.
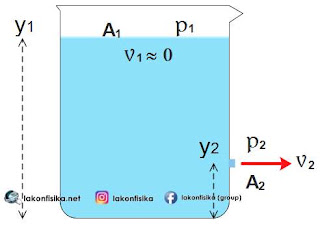
Pada gambar di atas, ada 2 penampang, yaitu permukaan cairan bagian atas $\left( {{A}_{1}} \right)$ dan permukaan air di bagian bocor $\left( {{A}_{2}} \right)$. Lubang kebocoran sangat kecil sehingga ${{A}_{2}}\ll {{A}_{1}}$, dan menurut persamaan kontinuitas dapat diasumsikan nilai ${{v}_{1}}\ll {{v}_{2}}$ atau nilai ${{v}_{1}}\approx 0$ (sangat kecil dan mendekati nol). Selanjutnya, pada penampang ${{A}_{1}}$ dan ${{A}_{2}}$, permukaan cairan terbuka sehingga mendapat tekanan yang sama, yaitu tekanan udara bebas ${{p}_{1}}={{p}_{2}}$. Berdasarkan kondisi fisis tersebut, maka persamaan Bernoulli dapat ditulis sebagai berikut:
$\begin{align}
& {{{p}_{1}}}+{\frac{1}{2}\rho \,v_{1}^{2}}+\rho \,g\,{{y}_{1}}=\ {{{p}_{2}}}\ +\frac{1}{2}\rho \,v_{2}^{2}+\rho \,g\,{{y}_{2}} \\
& {\rho }\,g\,{{y}_{1}}=\ \frac{1}{2}{\rho }\,v_{2}^{2}+{\rho }\,g\,{{y}_{2}} \\
& \frac{1}{2}\,v_{2}^{2}=g\,\left( {{y}_{1}} -{{y}_{2}} \right) \\
& v_{2}^{2}=2g\,\left( {{y}_{1}} -{{y}_{2}} \right) \\
\end{align}$
$ $
${{v}_{2}}=\sqrt{2g\,\left( {{y}_{1}} -{{y}_{2}} \right)}\ldots \ldots \ldots \ldots \ldots \left( 4 \right)$
Persamaan 4 untuk mencari kecepatan aliran pada kebocoran tabung tersebut, dikenal sebagai Teorema Torricelli.
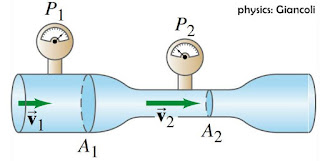
Pipa venturimeter menggunakan dua penampang yang berbeda ${{A}_{1}}$ dan ${{A}_{2}}$. Aliran fluida yang melewati ${{A}_{1}}$ dan ${{A}_{2}}$ memiliki posisi ketinggian yang sama ${{y}_{1}}={{y}_{2}}$. Pada masing-masing penampang diukur tekanannya, yaitu ${{p}_{1}}$ dan ${{p}_{2}}$. Nah, selanjutnya berdasarkan kondisi fisis tersebut dapat diuraikan persamaan Bernoulli berikut ini.
$\begin{align}
& {{p}_{1}}+\frac{1}{2}\rho \,v_{1}^{2}+{\rho \,g\,{{y}_{1}}}=\ {{p}_{2}}+\frac{1}{2}\rho \,v_{2}^{2}+{\rho \,g\,{{y}_{2}}} \\
& {{p}_{1}}+\frac{1}{2}\rho \,v_{1}^{2}={{p}_{2}}+\frac{1}{2}\rho \,v_{2}^{2} \\
& {{p}_{1}}-{{p}_{2}}=\frac{1}{2}\rho \ v_{2}^{2}\,-\ \frac{1}{2}\rho \ v_{1}^{2}\, \\
\end{align}$
Berdasarkan persamaan kontinuitas, nilai ${{v}_{2}}=\frac{{{A}_{1}}}{{{A}_{2}}}{{v}_{1}}$, dan substitusikan ke persamaan di atas.
$\begin{align}
& {{p}_{1}}-{{p}_{2}}=\frac{1}{2}\rho \ \left( \frac{{{A}_{1}}}{{{A}_{2}}}{{v}_{1}} \right){{\,}^{2}}-\ \frac{1}{2}\rho \ v_{1}^{2}\, \\
& {{p}_{1}}-{{p}_{2}}=\frac{1}{2}\rho \ v_{1}^{2}\left( {{\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}-1 \right) \\
\end{align}$
$ $
$v_{1}^{2}=\frac{2\left( {{p}_{1}}-{{p}_{2}} \right)}{\rho \left( {{\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}-1 \right)}\ldots \ldots \ldots \ldots \ldots \left( 5 \right)$
Saat pesawat pada posisi terbang, terjadi aliran udara di bagian pesawat tersebut, di bagian atas sayap $\left( {{v}_{a}} \right)$ dan di bagian bawah sayap $\left( {{v}_{b}} \right)$. Di penampang atas pesawat ada tekanan udara $\left( {{p}_{a}} \right)$, begitu pula di penampang bawah pesawat $\left( {{p}_{b}} \right)$. Sedangkan posisi ketinggian bagian atas dan bagian bawah pesawat diasumsikan sama.
Jika pesawat akan naik ke posisi ketinggian tertentu, maka pesawat membutuhkan gaya angkat $\left( {{F}_{A}} \right)$ dengan cara mengatur posisi sayap sedemikian rupa sehingga ${{v}_{b}}<{{v}_{a}}$ dan ${{p}_{b}}>{{p}_{a}}$. Kondisi tersebut sesuai dengan prinsip Bernoulli, jika aliran udara di penampang bawah sayap rendah, maka tekanan udara akan menjadi tinggi. Sedangkan pada penampang atas sayap mendapat tekanan yang kecil karena kecepatan aliran udara tinggi. Perbedaan tekanan ${{p}_{b}}$ dan ${{p}_{a}}$ inilah yang menyebabkan munculnya gaya angkat $\left( {{F}_{A}} \right)$ pada pesawat. Dengan asumsi luas penampang sayap pesawat adalah $A$, maka:
$\begin{align}
& {{F}_{A}}=\Delta p\,\cdot A \\
& {{F}_{A}}=\left( {{p}_{b}}-{{p}_{a}} \right)\ A \\
\end{align}$.
berdasarkan persamaan Bernoulli, nilai $\Delta p$ adalah:
$\begin{align}
& {{p}_{b}}+\frac{1}{2}\rho \,v_{b}^{2}+{\rho \,g\,{{y}_{b}}}=\ {{p}_{a}}+\frac{1}{2}\rho \,v_{a}^{2}+{\rho \,g\,{{y}_{a}}} \\
& {{p}_{b}}+\frac{1}{2}\rho \,v_{b}^{2}={{p}_{a}}+\frac{1}{2}\rho \,v_{a}^{2} \\
& {{p}_{b}}-{{p}_{a}}=\frac{1}{2}\rho \ v_{a}^{2}\,-\ \frac{1}{2}\rho \ v_{b}^{2}\, \\
& {{p}_{b}}-{{p}_{a}}=\frac{1}{2}\rho \ \left( v_{a}^{2}-v_{b}^{2}\, \right)\, \\
\end{align}$
sehingga diperoleh persamaan gaya angkat:
${{F}_{A}}=\left( {{p}_{b}}-{{p}_{a}} \right)\ A$
${{F}_{A}}=\frac{1}{2}\rho \ \left( v_{a}^{2}-v_{b}^{2}\, \right)\ A\ldots \ldots \ldots \ldots \ldots \left( 6 \right)$
Untuk lebih memahami dan contoh soal Fluida Dinamis dan Hukum Bernoulli, silakan temen-temen bisa melihat soal latihan Hukum Bernoulli berikut ini.
Nah untuk melakukan analisis fluida yang riil, pasti banyak parameter yang diperhatikan, sehingga untuk Fisika SMA Kelas 11 hanya dipelajari materi fisika dasar dengan kondisi fluida ideal. Yang dimaksud fluida ideal ini adalah fluida yang diasumsikan memiliki karakteristik aliran stabil (steady flow), aliran yang tidak terkompresi (incompressible flow), aliran yang tidak kental (nonviscous flow), dan aliran yang tidak berotasi (irrotational flow). Pada materi Fisika SMA Kelas 11, konsep fluida dinamis memiliki dua topik bahasan utama yaitu konsep kontinuitas aliran (debit aliran) dan konsep Hukum Bernoulli. Selain itu, akan dibahas pula apikasi Hukum Bernoulli antara lain Teorema Torricelli tentang tabung bocor, semprotan nyamuk, sayap pesawat terbang, dan venturimeter. Soal pada topik-topik ini bisa saling dikombinasikan sehingga memenuhi karakteristik model soal HOTS fisika. Sekarang langsung saja kita pelajari bersama konsep dan contoh soal Fluida Dinamis dan Hukum Bernoulli pada materi Fisika SMA Kelas 11.
1. Persamaan Kontinuitas – Debit Aliran Fluida
Sekarang coba kita pahami bersama aliran laminer fluida yang stabil seperti gambar di bawah. Fluida mengalir dalam pipa tertutup yang berbeda luas penampangnya. Untuk memahami kecepatan aliran fluida, kita mulai dari pemahaman laju massa fluida yang melewati penampang 1 $\left( {{A}_{1}} \right)$ dan penampang 2 $\left( {{A}_{2}} \right)$. Dalam kondisi pipa tertutup dan tidak ada fluida yang masuk atau keluar (kebocoran), maka aliran massa fluida $\left( \Delta m \right)$ tiap satuan waktu $\left( \Delta t \right)$ bersifat konstan.$\frac{\Delta {{m}_{1}}}{\Delta t}=\frac{\Delta {{m}_{2}}}{\Delta t}\ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
Pada gambar di atas, volume fluida yang melewati penampang 1 $\left( {{A}_{1}} \right)$ selama selang waktu $\left( \Delta t \right)$ adalah ${{A}_{1}}\ \Delta {{l}_{1}}$, dengan nilai $\Delta {{l}_{1}}$ adalah perpindahan massa fluida selama $\Delta t$. Fluida yang melewati ${{A}_{1}}$ memiliki massa jenis ${{\rho }_{1}}$ dengan kecepatan aliran fluida sebesar ${{v}_{1}}={}^{\Delta {{l}_{1}}}/{}_{\Delta t}$. Sehingga laju aliran massa fluida dapat diturunkan menjadi persamaan:
$\frac{\Delta {{m}_{1}}}{\Delta t}=\frac{{{\rho }_{1}}\ \Delta {{V}_{1}}}{\Delta t}=\frac{{{\rho }_{1}}\ {{A}_{1}}\ \Delta {{l}_{1}}}{\Delta t}={{\rho }_{1}}\ {{A}_{1}}\ {{v}_{1}}$
Dengan analisis yang sama, laju aliran massa pada penampang 2 adalah ${{\rho }_{2}}\ {{A}_{2}}\ {{v}_{2}}$, sehingga persamaan 1 tentang laju aliran massa fluida dapat dituliskan sebagai berikut:
$\begin{align}
& \frac{\Delta {{m}_{1}}}{\Delta t}=\frac{\Delta {{m}_{2}}}{\Delta t} \\
& {{\rho }_{1}}\ {{A}_{1}}\ {{v}_{1}}={{\rho }_{2}}\ {{A}_{2}}\ {{v}_{2}} \\
\end{align}$
Nah, di awal kita sudah batasi untuk jenis fluida ideal yang bersifat incompressible flow, artinya meskipun pipa berbeda penampang, massa jenis fluida $\rho $ tidak berubah atau konstan. Sehingga $\rho $ dapat dieliminasi. Sehingga dapat dinyatakan menjadi persamaan 2 berikut ini, yang disebut juga sebagai Persamaan Kontinuitas.
${{A}_{1}}\ {{v}_{1}}={{A}_{2}}\ {{v}_{2}}\ldots \ldots \ldots \ldots \ldots \left( 2 \right)$
Karena $v={}^{\Delta l}/{}_{\Delta t}$, maka persamaan 2 juga dapat dinyatakan sebagai laju volume fluida atau debit aliran fluida $\left( Q \right)$ yang konstan.
$\begin{align}
& {{A}_{1}}\ {{v}_{1}}={{A}_{2}}\ {{v}_{2}} \\
& {{A}_{1}}\ \frac{\Delta {{l}_{1}}}{\Delta t}={{A}_{2}}\ \frac{\Delta {{l}_{2}}}{\Delta t} \\
& \frac{\Delta {{V}_{1}}}{\Delta t}=\frac{\Delta {{V}_{2}}}{\Delta t} \\
& {{Q}_{1}}={{Q}_{2}} \\
\end{align}$
Contoh Soal Persamaan Kontinuitas
Sebuah pipa mempunyai dua penampang yang berbeda. Luas penampang pada posisi 1 dan 2 masing-masing adalah 600 cm2 dan 400 cm2. Laju aliran pada posisi 1 adalah 20 m/s. Tentukan debit aliran, laju aliran, dan volume air yang melewati posisi 2 dalam selang waktu 5 menit!
Jawab:
$\begin{align}
& {{A}_{1}}=600\ c{{m}^{2}}=6\times {{10}^{-2}}\ {{m}^{2}} \\
& {{A}_{2}}=400\ c{{m}^{2}}=4\times {{10}^{-2}}\ {{m}^{2}} \\
& {{v}_{1}}=20\ {}^{m}/{}_{s} \\
& t=5\ menit=300\ s \\
\end{align}$
$\begin{align}
& Q={{A}_{1}}\ {{v}_{1}} \\
& Q=6\times {{10}^{-2}}\ \cdot \ 20 \\
& Q=120\times {{10}^{-2}}\ {}^{{{m}^{3}}}/{}_{s}=12\ {}^{d{{m}^{3}}}/{}_{s}=12{}^{L}/{}_{s} \\
\end{align}$
Debit aliran fluida adalah 12 L/s.
$\begin{align}
& {{A}_{2}}\ {{v}_{2}}={{A}_{1}}\ {{v}_{1}} \\
& 4\times {{10}^{-2}}\ \cdot \ {{v}_{2}}=6\times {{10}^{-2}}\ \cdot \ 20 \\
& {{v}_{2}}=\frac{120}{4}=30\ {}^{m}/{}_{s} \\
\end{align}$
Laju aliran fluida pada penampang 2 adalah 30 m/s.
$\begin{align}
& Q=\frac{\Delta V}{\Delta t} \\
& \Delta V=Q\ \Delta t \\
& \Delta V=12\ \cdot \ 300=3600\ L \\
\end{align}$
Volume fluida yang mengalir pada penampang 2 selama 5 menit adalah 3600 L..
$\begin{align}
& {{A}_{1}}=600\ c{{m}^{2}}=6\times {{10}^{-2}}\ {{m}^{2}} \\
& {{A}_{2}}=400\ c{{m}^{2}}=4\times {{10}^{-2}}\ {{m}^{2}} \\
& {{v}_{1}}=20\ {}^{m}/{}_{s} \\
& t=5\ menit=300\ s \\
\end{align}$
$\begin{align}
& Q={{A}_{1}}\ {{v}_{1}} \\
& Q=6\times {{10}^{-2}}\ \cdot \ 20 \\
& Q=120\times {{10}^{-2}}\ {}^{{{m}^{3}}}/{}_{s}=12\ {}^{d{{m}^{3}}}/{}_{s}=12{}^{L}/{}_{s} \\
\end{align}$
Debit aliran fluida adalah 12 L/s.
$\begin{align}
& {{A}_{2}}\ {{v}_{2}}={{A}_{1}}\ {{v}_{1}} \\
& 4\times {{10}^{-2}}\ \cdot \ {{v}_{2}}=6\times {{10}^{-2}}\ \cdot \ 20 \\
& {{v}_{2}}=\frac{120}{4}=30\ {}^{m}/{}_{s} \\
\end{align}$
Laju aliran fluida pada penampang 2 adalah 30 m/s.
$\begin{align}
& Q=\frac{\Delta V}{\Delta t} \\
& \Delta V=Q\ \Delta t \\
& \Delta V=12\ \cdot \ 300=3600\ L \\
\end{align}$
Volume fluida yang mengalir pada penampang 2 selama 5 menit adalah 3600 L..
2. Persamaan Bernoulli – Hukum Bernoulli
Tinjauan lain untuk menganalisis aliran fluida (untuk fluida ideal) adalah melalui seluruh kerja yang terjadi pada fluida. Kemungkinan aliran fluida selain melewati penampang yang berbeda, juga melewati ketinggian yang berbeda seperti gambar di bawah. Setelah kita melakukan analisis dari luas penampang $\left( A \right)$ dan kecepatan aliran $\left( v \right)$, selanjutnya akan dimasukkan besaran lain yaitu tekanan $\left( p \right)$ serta posisi ketinggian $\left( h \right)$.Pada gambar di atas, fluida memasuki ${{A}_{1}}$, kemudian mengalir sejauh $\Delta {{l}_{1}}$dan mendesak fluida pada ${{A}_{2}}$ untuk bergeser sejauh $\Delta {{l}_{2}}$. Fluida di sebelah kiri ${{A}_{1}}$ menekan fluida dalam luasan tersebut sebesar ${{p}_{1}}$ dan melakukan kerja sebesar:
${{W}_{1}}={{F}_{1}}\ \Delta {{l}_{1}}={{p}_{1}}\ {{A}_{1}}\ \Delta {{l}_{1}}\ldots \ldots \ldots \ldots \ldots $ dengan nilai $p=\frac{F}{A}$
Pada penampang 2, kerja yang dilakukan sebesar ${{W}_{2}}=-{{p}_{2}}\ {{A}_{2}}\ \Delta {{l}_{2}}$, tanda negatif disebabkan arah gaya berlawanan dengan arah perpindahan fluida. Selain itu, kerja juga dilakukan pada fluida oleh gaya gravitasi. Fluida mengalir dari ${{A}_{1}}$ menuju ${{A}_{2}}$ dan mengalami perpindahan posisi ketinggian dari ${{y}_{1}}$ menuju ${{y}_{2}}$ akibat kerja yang dilakukan gaya gravitasi $\left( {{W}_{3}} \right)$:
${{W}_{3}}=-m\,g\left( {{y}_{2}}-{{y}_{1}} \right)$
Selanjutnya total kerja yang terjadi pada fluida adalah:
$\begin{align}
& W={{W}_{1}}+{{W}_{2}}+{{W}_{3}} \\
& W={{p}_{1}}\ {{A}_{1}}\ \Delta {{l}_{1}}+\left( -{{p}_{2}}\ {{A}_{2}}\ \Delta {{l}_{2}} \right)+\left( -m\,g\left( {{y}_{2}}-{{y}_{1}} \right) \right) \\
\end{align}$
Karena kerja total sistem sama dengan perubahan energi kinetik, maka:
$\frac{1}{2}m\,v_{2}^{2}-\frac{1}{2}m\,v_{1}^{2}={{p}_{1}}\ {{A}_{1}}\ \Delta {{l}_{1}}-{{p}_{2}}\ {{A}_{2}}\ \Delta {{l}_{2}}-m\,g\,{{y}_{2}}+m\,g\,{{y}_{1}}$
Untuk fluida ideal (incompressible), nilai ${{A}_{1}}\ \Delta {{l}_{1}}={{A}_{2}}\ \Delta {{l}_{2}}=A\ \Delta l=V$(volume fluida). Persamaan di atas dapat dibagi dengan $V$ sehingga diperoleh:
$\begin{align}
& \frac{1}{2}\frac{m}{V}\,v_{2}^{2}-\frac{1}{2}\frac{m}{V}\,v_{1}^{2}={{p}_{1}}\ -{{p}_{2}}\ -\frac{m}{V}\,g\,{{y}_{2}}+\frac{m}{V}\,g\,{{y}_{1}} \\
& \frac{1}{2}\rho \,v_{2}^{2}-\frac{1}{2}\rho \,v_{1}^{2}={{p}_{1}}\ -{{p}_{2}}\ -\rho \,g\,{{y}_{2}}+\rho \,g\,{{y}_{1}} \\
\end{align}$
$ $
${{p}_{1}}+\frac{1}{2}\rho \,v_{1}^{2}+\rho \,g\,{{y}_{1}}=\ {{p}_{2}}\ +\frac{1}{2}\rho \,v_{2}^{2}+\rho \,g\,{{y}_{2}}\,\ldots \ldots \ldots \ldots \ldots \left( 3 \right)$
Persamaan 3 disebut sebagai Persamaan Bernoulli. Secara umum, hukum Bernoulli menyatakan bahwa jika kecepatan aliran fluida tinggi, maka tekanannya rendah dan jika kecepatan aliran fluida renda, maka tekanannya tinggi.
Contoh Soal Hukum Bernoulli
Dalam suatu rumah diterapkan sistem sirkulasi air panas. Air dipompa pada kecepatan 0,5 m/s melewati pipa dengan penampang berdiameter 4 cm yang berada di basement. Berapakah kecepatan aliran dan tekanan air pada pipa berdiameter 2,6 cm yang berada di lantai 2 (5 meter dari basement)? (Asumsikan pipa tunggal dan tidak bercabang)
Jawab:
$\begin{align}
& {{r}_{1}}=0,02\ m \\
& {{r}_{2}}=0,013\ m \\
& {{v}_{1}}=0,5\,\,{}^{m}/{}_{s} \\
& {{p}_{1}}=3\ atm=3\times {{10}^{5}}\ {}^{N}/{}_{{{m}^{2}}} \\
& {{y}_{1}}={{0}_{\left( basement \right)}} \\
& {{y}_{2}}=5\ m \\
\end{align}$
$\begin{align}
& {{A}_{1}}\ {{v}_{1}}={{A}_{2}}\ {{v}_{2}} \\
& {{v}_{2}}=\frac{{{A}_{1}}}{{{A}_{2}}}{{v}_{1}} \\
& {{v}_{2}}=\frac{\pi {{r}_{1}}^{2}}{\pi {{r}_{2}}^{2}}{{v}_{1}} \\
& {{v}_{2}}=\frac{{{\left( 0,02 \right)}^{2}}}{{{\left( 0,013 \right)}^{2}}}\cdot 0,5 \\
& {{v}_{2}}=1,2{\,m}/{s}\; \\
\end{align}$
$\begin{align}
& {{p}_{1}}+\frac{1}{2}\rho \,v_{1}^{2}+\rho \,g\,{{y}_{1}}=\ {{p}_{2}}\ +\frac{1}{2}\rho \,v_{2}^{2}+\rho \,g\,{{y}_{2}} \\
& {{p}_{2}}={{p}_{1}}+\frac{1}{2}\rho \,\left( v_{1}^{2}-v_{2}^{2} \right)+\rho \,g\,\left( {{y}_{1}}-{{y}_{2}} \right) \\
& {{p}_{2}}=\left( 3\times {{10}^{5}} \right)+\frac{1}{2}\cdot {{10}^{3}}\,\left( {{\left( 0,5 \right)}^{2}}-{{\left( 1,2 \right)}^{2}} \right)+{{10}^{3}}\cdot 10\cdot \left( 0-5 \right) \\
& {{p}_{2}}=\left( 3\times {{10}^{5}} \right)-\left( 6\times {{10}^{2}} \right)-\left( 0,5\times {{10}^{5}} \right) \\
& {{p}_{2}}\approx 2,5\times {{10}^{5}}\ {N}/{{{m}^{2}}}\;\approx 2,5\ atm \\
\end{align}$
$\begin{align}
& {{r}_{1}}=0,02\ m \\
& {{r}_{2}}=0,013\ m \\
& {{v}_{1}}=0,5\,\,{}^{m}/{}_{s} \\
& {{p}_{1}}=3\ atm=3\times {{10}^{5}}\ {}^{N}/{}_{{{m}^{2}}} \\
& {{y}_{1}}={{0}_{\left( basement \right)}} \\
& {{y}_{2}}=5\ m \\
\end{align}$
$\begin{align}
& {{A}_{1}}\ {{v}_{1}}={{A}_{2}}\ {{v}_{2}} \\
& {{v}_{2}}=\frac{{{A}_{1}}}{{{A}_{2}}}{{v}_{1}} \\
& {{v}_{2}}=\frac{\pi {{r}_{1}}^{2}}{\pi {{r}_{2}}^{2}}{{v}_{1}} \\
& {{v}_{2}}=\frac{{{\left( 0,02 \right)}^{2}}}{{{\left( 0,013 \right)}^{2}}}\cdot 0,5 \\
& {{v}_{2}}=1,2{\,m}/{s}\; \\
\end{align}$
$\begin{align}
& {{p}_{1}}+\frac{1}{2}\rho \,v_{1}^{2}+\rho \,g\,{{y}_{1}}=\ {{p}_{2}}\ +\frac{1}{2}\rho \,v_{2}^{2}+\rho \,g\,{{y}_{2}} \\
& {{p}_{2}}={{p}_{1}}+\frac{1}{2}\rho \,\left( v_{1}^{2}-v_{2}^{2} \right)+\rho \,g\,\left( {{y}_{1}}-{{y}_{2}} \right) \\
& {{p}_{2}}=\left( 3\times {{10}^{5}} \right)+\frac{1}{2}\cdot {{10}^{3}}\,\left( {{\left( 0,5 \right)}^{2}}-{{\left( 1,2 \right)}^{2}} \right)+{{10}^{3}}\cdot 10\cdot \left( 0-5 \right) \\
& {{p}_{2}}=\left( 3\times {{10}^{5}} \right)-\left( 6\times {{10}^{2}} \right)-\left( 0,5\times {{10}^{5}} \right) \\
& {{p}_{2}}\approx 2,5\times {{10}^{5}}\ {N}/{{{m}^{2}}}\;\approx 2,5\ atm \\
\end{align}$
3. Penerapan Hukum Bernoulli – Teorema Torricelli (Tabung Bocor)
Salah satu penerapan persamaan Bernoulli adalah untuk mencari kecepatan aliran cairan pada tabung bocor. Gambar di bawah ini adalah ilustrasinya.Pada gambar di atas, ada 2 penampang, yaitu permukaan cairan bagian atas $\left( {{A}_{1}} \right)$ dan permukaan air di bagian bocor $\left( {{A}_{2}} \right)$. Lubang kebocoran sangat kecil sehingga ${{A}_{2}}\ll {{A}_{1}}$, dan menurut persamaan kontinuitas dapat diasumsikan nilai ${{v}_{1}}\ll {{v}_{2}}$ atau nilai ${{v}_{1}}\approx 0$ (sangat kecil dan mendekati nol). Selanjutnya, pada penampang ${{A}_{1}}$ dan ${{A}_{2}}$, permukaan cairan terbuka sehingga mendapat tekanan yang sama, yaitu tekanan udara bebas ${{p}_{1}}={{p}_{2}}$. Berdasarkan kondisi fisis tersebut, maka persamaan Bernoulli dapat ditulis sebagai berikut:
$\begin{align}
& {{{p}_{1}}}+{\frac{1}{2}\rho \,v_{1}^{2}}+\rho \,g\,{{y}_{1}}=\ {{{p}_{2}}}\ +\frac{1}{2}\rho \,v_{2}^{2}+\rho \,g\,{{y}_{2}} \\
& {\rho }\,g\,{{y}_{1}}=\ \frac{1}{2}{\rho }\,v_{2}^{2}+{\rho }\,g\,{{y}_{2}} \\
& \frac{1}{2}\,v_{2}^{2}=g\,\left( {{y}_{1}} -{{y}_{2}} \right) \\
& v_{2}^{2}=2g\,\left( {{y}_{1}} -{{y}_{2}} \right) \\
\end{align}$
$ $
${{v}_{2}}=\sqrt{2g\,\left( {{y}_{1}} -{{y}_{2}} \right)}\ldots \ldots \ldots \ldots \ldots \left( 4 \right)$
Persamaan 4 untuk mencari kecepatan aliran pada kebocoran tabung tersebut, dikenal sebagai Teorema Torricelli.
4. Penerapan Hukum Bernoulli – Venturimeter
Venturimeter digunakan untuk mengukur kecepatan aliran fluida yang memanfaatkan prinsip Bernoulli. Gambar di bawah ini adalah ilustrasi venturimeter.Pipa venturimeter menggunakan dua penampang yang berbeda ${{A}_{1}}$ dan ${{A}_{2}}$. Aliran fluida yang melewati ${{A}_{1}}$ dan ${{A}_{2}}$ memiliki posisi ketinggian yang sama ${{y}_{1}}={{y}_{2}}$. Pada masing-masing penampang diukur tekanannya, yaitu ${{p}_{1}}$ dan ${{p}_{2}}$. Nah, selanjutnya berdasarkan kondisi fisis tersebut dapat diuraikan persamaan Bernoulli berikut ini.
$\begin{align}
& {{p}_{1}}+\frac{1}{2}\rho \,v_{1}^{2}+{\rho \,g\,{{y}_{1}}}=\ {{p}_{2}}+\frac{1}{2}\rho \,v_{2}^{2}+{\rho \,g\,{{y}_{2}}} \\
& {{p}_{1}}+\frac{1}{2}\rho \,v_{1}^{2}={{p}_{2}}+\frac{1}{2}\rho \,v_{2}^{2} \\
& {{p}_{1}}-{{p}_{2}}=\frac{1}{2}\rho \ v_{2}^{2}\,-\ \frac{1}{2}\rho \ v_{1}^{2}\, \\
\end{align}$
Berdasarkan persamaan kontinuitas, nilai ${{v}_{2}}=\frac{{{A}_{1}}}{{{A}_{2}}}{{v}_{1}}$, dan substitusikan ke persamaan di atas.
$\begin{align}
& {{p}_{1}}-{{p}_{2}}=\frac{1}{2}\rho \ \left( \frac{{{A}_{1}}}{{{A}_{2}}}{{v}_{1}} \right){{\,}^{2}}-\ \frac{1}{2}\rho \ v_{1}^{2}\, \\
& {{p}_{1}}-{{p}_{2}}=\frac{1}{2}\rho \ v_{1}^{2}\left( {{\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}-1 \right) \\
\end{align}$
$ $
$v_{1}^{2}=\frac{2\left( {{p}_{1}}-{{p}_{2}} \right)}{\rho \left( {{\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}-1 \right)}\ldots \ldots \ldots \ldots \ldots \left( 5 \right)$
5. Penerapan Hukum Bernoulli – Gaya Angkat Pesawat Terbang
Sayap pesawat terbang memanfaatkan prinsip dasar Hukum Bernoulli. Perlu dipahami bahwa pesawat berada di dalam fluida saat terbang, yaitu udara (dalam wujud gas). Gambar di bawah ini adalah ilustrasi sebuah pesawat terbang.Saat pesawat pada posisi terbang, terjadi aliran udara di bagian pesawat tersebut, di bagian atas sayap $\left( {{v}_{a}} \right)$ dan di bagian bawah sayap $\left( {{v}_{b}} \right)$. Di penampang atas pesawat ada tekanan udara $\left( {{p}_{a}} \right)$, begitu pula di penampang bawah pesawat $\left( {{p}_{b}} \right)$. Sedangkan posisi ketinggian bagian atas dan bagian bawah pesawat diasumsikan sama.
Jika pesawat akan naik ke posisi ketinggian tertentu, maka pesawat membutuhkan gaya angkat $\left( {{F}_{A}} \right)$ dengan cara mengatur posisi sayap sedemikian rupa sehingga ${{v}_{b}}<{{v}_{a}}$ dan ${{p}_{b}}>{{p}_{a}}$. Kondisi tersebut sesuai dengan prinsip Bernoulli, jika aliran udara di penampang bawah sayap rendah, maka tekanan udara akan menjadi tinggi. Sedangkan pada penampang atas sayap mendapat tekanan yang kecil karena kecepatan aliran udara tinggi. Perbedaan tekanan ${{p}_{b}}$ dan ${{p}_{a}}$ inilah yang menyebabkan munculnya gaya angkat $\left( {{F}_{A}} \right)$ pada pesawat. Dengan asumsi luas penampang sayap pesawat adalah $A$, maka:
$\begin{align}
& {{F}_{A}}=\Delta p\,\cdot A \\
& {{F}_{A}}=\left( {{p}_{b}}-{{p}_{a}} \right)\ A \\
\end{align}$.
berdasarkan persamaan Bernoulli, nilai $\Delta p$ adalah:
$\begin{align}
& {{p}_{b}}+\frac{1}{2}\rho \,v_{b}^{2}+{\rho \,g\,{{y}_{b}}}=\ {{p}_{a}}+\frac{1}{2}\rho \,v_{a}^{2}+{\rho \,g\,{{y}_{a}}} \\
& {{p}_{b}}+\frac{1}{2}\rho \,v_{b}^{2}={{p}_{a}}+\frac{1}{2}\rho \,v_{a}^{2} \\
& {{p}_{b}}-{{p}_{a}}=\frac{1}{2}\rho \ v_{a}^{2}\,-\ \frac{1}{2}\rho \ v_{b}^{2}\, \\
& {{p}_{b}}-{{p}_{a}}=\frac{1}{2}\rho \ \left( v_{a}^{2}-v_{b}^{2}\, \right)\, \\
\end{align}$
sehingga diperoleh persamaan gaya angkat:
${{F}_{A}}=\left( {{p}_{b}}-{{p}_{a}} \right)\ A$
${{F}_{A}}=\frac{1}{2}\rho \ \left( v_{a}^{2}-v_{b}^{2}\, \right)\ A\ldots \ldots \ldots \ldots \ldots \left( 6 \right)$
Untuk lebih memahami dan contoh soal Fluida Dinamis dan Hukum Bernoulli, silakan temen-temen bisa melihat soal latihan Hukum Bernoulli berikut ini.