Konsep dan Contoh Soal Energi Potensial Listrik – Fisika SMA Kelas 12

Bagaimana kajian tentang energi yang ada pada muatan listrik? Tentunya tidak lepas dari energi kinetik, energi potensial listrik, dan prinsip kekekalan energi. Konsep energi dapat digunakan untuk menganalisis fenomena kelistrikan selain menggunakan konsep gaya elektrostatik atau medan listrik. Untuk beberapa kasus fenomena kelistrikan, konsep energi lebih mudah digunakan untuk menyelesaikan permasalahan (soal).

Pada materi fisika SMA kelas 12, fokus pembahasan adalah tentang penggunaan konsep energi untuk menyelesaikan soal-soal yang berkaitan dengan energi potensial listrik. Agar mampu menyelesaikan soal-soal tersebut, harus dipahami beberapa konsep berikut ini:
a) energi potensial listrik
b) potensial listrik dan beda potensial
c) hubungan antara potensial listrik dan medan listrik
d) potensial listrik akibat beberapa muatan titik (point charges)

1. Konsep Energi Potensial Listrik

Energi potensial dapat didefinisikan hanya untuk gaya konservatif. Jika ada muatan listrik yang berpindah posisi, maka ada kerja $\left( W \right)$ yang dilakukan oleh gaya elektrostatik pada muatan tersebut. Ada interaksi berupa gaya elektrostatik yang besarnya bergantung posisi muatan tersebut. Sehingga gaya elektrostatik termasuk jenis gaya konservatif dan dapat didefinisikan energi potensial dari gaya tersebut. Sebagai contoh adalah fenomena berpindahnya muatan positif pada gambar di bawah ini.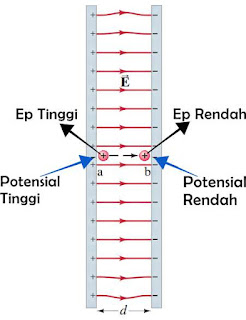

Ilustrasi Energi Potensial Listrik pada Muatan

Pada gambar di atas, muatan positif $q$ berpindah posisi dari titik a ke titik b dalam area medan listrik. Perpindahan terebut disebabkan adanya gaya tolak elektrostatik ke arah b pada muatan akibat pengaruh medan listrik. Posisi a merupakan titik dengan potensial tinggi, sehingga muatan $q$ memiliki energi potensial $\left( {{E}_{p}} \right)$ yang tinggi. Sedangkan titik b merupakan posisi dengan potensial rendah, sehingga muatan $q$ memiliki energi potensial $\left( Ep \right)$ yang rendah. Jadi muatan $q$ berpindah dari potensial tinggi $\left( {{V}_{a}} \right)$ ke potensial yang lebih rendah $\left( {{V}_{b}} \right)$.

Setelah kita pahami bersama fenomena fisis pada perpindahan muatan $\left( q \right)$ tersebut, sekarang coba kita pahami bagaimana hubungan matematis antara medan listrik $\left( E \right)$, gaya elektrostatik $\left( F \right)$, dam kerja $\left( W \right)$. Untuk medan listrik homogen dalam area titik a dan b, kerja yang dilakukan oleh gaya elektrostatik pada muatan adalah:

$W=F\,d$ dengan nilai $F=q\,E$, maka persamaan tersebut dapat dituliskan:

$W=q\,E\,d\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$

Perubahan energi potensial $\left( \Delta {{E}_{p}} \right)$ pada muatan merupakan negatif dari kerja yang dikerjakan $\left( -W \right)$ oleh gaya elektrostatik, sehingga hubungan antara masing-masing besaran adalah:

$\Delta Ep=-W$

$E{{p}_{b}}-E{{p}_{a}}=-q\,E\,d\quad \ldots \ldots \ldots \ldots \ldots \left( 2 \right)$

Berdasarkan fenomena fisis dan persamaan matematis yang sudah dijelaskan, dapat diketahui bahwa muatan $q$ mengalami penurunan besar energi potensial ketika berpindah dari titik a ke titik b. Perpindahan tersebut dipicu akibat adanya percepatan yang disebabkan oleh gaya elektrostatik. Artinya kecepatan muatan di titik b $\left( {{v}_{b}} \right)$ lebih besar dari pada di titik a $\left( {{v}_{a}} \right)$ atau dapat disimpulkan bahwa terjadi peningkatan energi kinetik $\left( Ek \right)$, yaitu $E{{k}_{b}}>E{{k}_{a}}$. Hal tersebut sesuai dengan prinsip hukum kekekalan energi mekanik pada gaya konservatif.

2. Konsep Potensial Listrik dan Beda Potensial

Potensial listrik didefinisikan sebagai besar energi potensial listrik per satuan muatan. Sebagai contoh pada gambar di atas, jika pada titik a muatan listrik positif memiliki energi potensial sebesar $E{{p}_{a}}$, maka besar potensial listrik di titik a $\left( {{V}_{a}} \right)$ adalah:

${{V}_{a}}=\frac{E{{p}_{a}}}{q}\quad \ldots \ldots \ldots \ldots \ldots \left( 3 \right)$ 

Sesuai konsep energi pada gaya konservatif, bahwa perubahan energi potensial $\left( \Delta {{E}_{p}} \right)$ pada muatan merupakan negatif dari kerja yang dikerjakan oleh gaya elektrostatik $\left( -{{W}_{ab}} \right)$, maka dapat dinyatakan hubungan persamaan berikut.

$\Delta Ep=-W$

$E{{p}_{b}}-E{{p}_{a}}=-{{W}_{ab}}$ 

$q{{V}_{b}}-q{{V}_{a}}=-{{W}_{ab}}$ 

$q\left( {{V}_{b}}-{{V}_{a}} \right)=-{{W}_{ab}}$ dengan nilai ${{V}_{b}}-{{V}_{a}}$ adalah beda potensial antara titik b dan a $\left( {{V}_{ba}} \right)$, maka:

$q\,{{V}_{ba}}=-{{W}_{ab}}\quad \ldots \ldots \ldots \ldots \ldots \left( 4 \right)$

Contoh Soal Energi Potensial Listrik

Asumsikan sebuah elektron bergerak dipercepat dari keadaan diam (plat a) menuju ke plat b dalam area dengan beda potensial ${{V}_{b}}-{{V}_{a}}={{V}_{ba}}={{V}_{ba}}=+5000\ volt$ seperti gambar di bawah ini. $\left( {{m}_{e}}=9,1\cdot {{10}^{-31}}\ kg \right)$ 

(a) Berapa besar perubahan energi potensial elektron?

(b) Berapa besar energi kinetik saat elektron sampai di plat b?

(c) Berapa besar kecepatan elektron saat sampai di plat b?

Jawab:

(a) Besar muatan elektron adalah ${{q}_{e}}=-1,6\times {{10}^{-19}}C$, maka perubahan energi potensial elektron adalah:


$\Delta Ep={{q}_{e}}\,{{V}_{ba}}$

$\Delta Ep=\left( -1,6\cdot {{10}^{-19}} \right)\cdot \left( 5\cdot {{10}^{3}} \right)$

$\Delta Ep=-8\cdot {{10}^{-16}}\ Joule$

Tanda minus (-) menandakan terjadi penurunan besar energi potensial. Nilai ${{V}_{ba}}$ bertanda positif karena ${{V}_{b}}>{{V}_{a}}$, sehingga elektron tertarik menuju plat positif (b) atau ditolak oleh plat negatif (a).


(b) Penurunan besar energi potensial menunjukkan bahwa ada energi potensial yang hilang dan berubah menjadi energi kinetik. Berdasarkan hukum kekekalan energi mekanik, $\Delta Ek+\Delta Ep=0$, maka:

$\Delta Ek=-\Delta Ep$

$E{{k}_{b}}-E{{k}_{a}}=-\Delta Ep$

$E{{k}_{b}}-0=-\Delta Ep$ (di plat a, elektron masih diam atau ${{v}_{a}}=0$, sehingga

$E{{k}_{a}}=0$)

$E{{k}_{b}}=-\left( -8\cdot {{10}^{-16}} \right)=8\cdot {{10}^{-16}}\ Joule$


(c) Berdasarkan jawaban nomor b, maka dapat kita uraikan hubungan persamaan berikut:

$E{{k}_{b}}=-\Delta Ep$

$\frac{1}{2}{{m}_{e}}{{v}_{b}}^{2}=-{{q}_{e}}\,{{V}_{ba}}$

${{v}_{b}}^{2}=\frac{-2{{q}_{e}}\,{{V}_{ba}}}{{{m}_{e}}}$

${{v}_{b}}=\sqrt{\frac{-2{{q}_{e}}\,{{V}_{ba}}}{{{m}_{e}}}}$

${{v}_{b}}=\sqrt{\frac{-2\left( -1,6\cdot {{10}^{-19}} \right)5\cdot {{10}^{3}}}{9,1\cdot {{10}^{-31}}}}$

${{v}_{b}}=4,2\cdot {{10}^{7}}\,{m}/{s}\;$

Jadi besar kecepatan elektron saat sampai di plat b adalah $4,2\cdot {{10}^{7}}\,{m}/{s}\;$.

3. Hubungan antara Potensial Listrik dan Medan Listrik

Potensial listrik merupakan besaran skalar, berbeda dengan medan listrik yang merupakan besaran vektor. Artinya untuk menentukan besar potensial listrik, tidak perlu melakukan analisis vektor (menggambar arah vektor kemudian mencari resultan). Walaupun berbeda jenis besaran, tetapi antara potensial listrik dan medan listrik memiliki hubungan dalam persamaan. 

Berdasarkan persamaan 1 $\left( W=q\,E\,d \right)$ dan persamaan 4 $\left( {{W}_{ab}}=-q\,{{V}_{ba}} \right)$, maka didapatkan hubungan persamaan berikut ini:

$-q\,{{V}_{ba}}=q\,E\,d$

${{V}_{ba}}=-E\,d$ atau $E=-\frac{{{V}_{ba}}}{d}\quad \ldots \ldots \ldots \ldots \ldots \left( 5 \right)$ 

Tanda minus (-) hanya menunjukkan bahwa arah medan listrik $\left( E \right)$ searah dengan penurunan potensial listrik. Jadi dalam perhitungan nilai besaran, tanda minus (-)bisa diabaikan.

Contoh Soal Hubungan antara Potensial Listrik dan Medan Listrik

Dua plat sejajar memiliki perbedaan potensial sebesar 50 V. Jika kedua plat terpisah dengan jarak 0,05 m, maka besar medan listrik di antara kedua plat tersebut adalah...

Jawab:

$E=\frac{{{V}_{ba}}}{d}$ 

$E=\frac{50}{0,05}=1000\ {V}/{m}\;$

Jika kita gambarkan arah medan listriknya adalah menuju potensial yang lebih rendah.

4. Konsep Potensial Listrik dari Muatan Titik

Seperti dengan munculnya medan listrik, setiap muatan titik menghasilkan potensial listrik pada suatu titik yang berjarak $r$ dari posisinya. Perbedaannya adalah potensial listrik merupakan besaran skalar dan nilainya dipengaruhi oleh jenis muatan (positif atau negatif). Besar potensial listrik ditentukan dari persamaan medan listrik yang dihasilkan muatan dengan teknik kalkulus atau dari hubungan persamaan 5. Sehingga didapatkan persamaan 6 berikut ini.

$V=k\frac{q}{r}\quad \ldots \ldots \ldots \ldots \ldots \left( 6 \right)$

Ilustrasi Potensial Listrik oleh 2 Muatan

Untuk menentukan besar potensial listrik pada suatu titik akibat beberapa muatan, maka perlu ditentukan masing-masing potensial listrik dari setiap muatan. Sebagai contoh gambar di atas, ada dua muatan ${{q}_{1}}$ dan ${{q}_{2}}$ sehingga muncul potensial listrik pada titik P. Karena potensial listrik merupakan besaran skalar, maka potensial total pada titik P hanya merupakan penjumlahan dari masing-masing potensial listrik dari muatan ${{q}_{1}}$ yaitu ${{V}_{1}}$ dan muatan ${{q}_{2}}$ yaitu ${{V}_{2}}$.

${{V}_{p}}=k\frac{{{q}_{1}}}{{{r}_{1}}}+k\frac{{{q}_{2}}}{{{r}_{2}}}$ 

${{V}_{p}}=k\left( \frac{{{q}_{1}}}{{{r}_{1}}}+\frac{{{q}_{2}}}{{{r}_{2}}} \right)\quad \ldots \ldots \ldots \ldots \ldots \left( 7 \right)$ 

Contoh Soal Potensial Listrik dari Muatan Titik

(1). Tentukan besar potensial listrik pada suatu titik yang berjarak 0,5 m (a) dari muatan $+20\,\mu C$, (b) dari muatan $-20\,\mu C$.

Jawab:

(a) Potensial listrik untuk muatan positif

$V=k\frac{q}{r}$ 

$V=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{5\cdot {{10}^{-1}}}$ 

$V=3,6\cdot {{10}^{5}}volt$ 

(b) Potensial listrik untuk muatan negatif

$V=k\frac{q}{r}$ 

$V=9\cdot {{10}^{9}}\frac{\left( -20\cdot {{10}^{-6}} \right)}{5\cdot {{10}^{-1}}}$ 

$V=-3,6\cdot {{10}^{5}}volt$ 

Berdasarkan jawaban a dan b, maka disimpulkan bahwa potensial listrik dapat bernilai positif atau negatif, bergantung jenis muatannya.

(2). Berapakah usaha minimum yang dikerjakan gaya eksternal untuk memindahkan muatan $q=3\,\mu C$ dari posisi yang sangat jauh $\left( r=\infty  \right)$ menuju posisi yang berjarak 0,5 m dari muatan $Q=20\,\mu C$?

Jawab:

Kita misalkan posisi awal berjarak ${{r}_{a}}=\infty $ dari muatan $Q$ dan posisi akhir berjarak ${{r}_{b}}=0,5\,m$ dari muatan $Q$.

$W=q\left( {{V}_{b}}-{{V}_{a}} \right)$ 

$W=q\left( k\frac{Q}{{{r}_{b}}}-k\frac{Q}{{{r}_{a}}} \right)$  (potensial disebabkan oleh muatan titik $Q$)

$W=k\,Q\,q\left( \frac{1}{{{r}_{b}}}-\frac{1}{{{r}_{a}}} \right)$

$W=\left( 9\cdot {{10}^{9}} \right)\,\left( 20\cdot {{10}^{-6}} \right)\,\left( 3\cdot {{10}^{-6}} \right)\left( \frac{1}{0,5}-\frac{1}{\infty } \right)$

$W=54\cdot {{10}^{-2}}\,\left( 2-0 \right)$

$W=108\cdot {{10}^{-2}}\,J=1,08\ J$ 

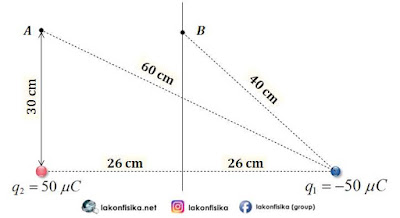
(3). Tentukan besar potensial listrik di masing-masing titik A dan B dari muatan listrik pada gambar di bawah ini!

Jawab:

Jarak masing-masing muatan dari titik A adalah ${{r}_{A1}}=0,6\,m$ dan ${{r}_{A2}}=0,3\,m$.

${{V}_{A}}={{V}_{A1}}+{{V}_{A2}}$ 

${{V}_{A}}=k\frac{{{q}_{1}}}{{{r}_{A1}}}+k\frac{{{q}_{2}}}{{{r}_{A2}}}$ 

${{V}_{A}}=9\cdot {{10}^{9}}\frac{\left( -50\cdot {{10}^{-6}} \right)}{0,6}+9\cdot {{10}^{9}}\frac{50\cdot {{10}^{-6}}}{0,3}$

${{V}_{A}}=-0,75\cdot {{10}^{6}}+1,5\cdot {{10}^{6}}$

${{V}_{A}}=7,5\cdot {{10}^{5}}\ volt$

Jarak masing-masing muatan dari titik B adalah ${{r}_{B1}}={{r}_{B2}}=0,4\,m$ karena merupakan sisi segitiga sama kaki.

${{V}_{B}}={{V}_{B1}}+{{V}_{B2}}$ 

${{V}_{B}}=k\frac{{{q}_{1}}}{{{r}_{B1}}}+k\frac{{{q}_{2}}}{{{r}_{B2}}}$ 

${{V}_{B}}=9\cdot {{10}^{9}}\frac{\left( -50\cdot {{10}^{-6}} \right)}{0,4}+9\cdot {{10}^{9}}\frac{50\cdot {{10}^{-6}}}{0,4}$

${{V}_{B}}=0$

Share this post