Konsep dan Contoh Soal Bola Konduktor (Hukum Gauss) – Fisika SMA Kelas 12
Jul 24, 2019
Edit
Hukum Gauss menyatakan bahwa jumlah fluks listrik dalam suatu permukaan tertutup sebanding dengan jumlah muatan listrik yang dilingkupi (dibungkus) oleh permukaan tersebut $\left( Q \right)$. Secara umum hubungan persamaan Hukum Gauss dinyatakan dalam persamaan 1 berikut ini.
$\int{E\,dA}=\frac{Q}{{{\varepsilon }_{o}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
 |
| Ilustrasi Permukaan Gauss pada Bola Konduktor |
Untuk menentukan besar medan listrik yang disebabkan oleh bola konduktor (jari-jari adalah $R$), maka perlu ditentukan terlebih dulu titik ujinya, yaitu di dalam bola, di permukaan bola, atau di luar bola. Setelah itu baru kita buat permukaan Gauss pada masing-masing titik uji tersebut dengan jari-jari sebesar $r$. Gambar di atas menunjukkan ilustrasi permukaan Gauss pada masing-masing daerah bola konduktor.
Sedangkan potensial listrik ditentukan berdasarkan hubungannya dengan medan listrik yaitu:
$\int\limits_{R}^{r}{dV}=\int\limits_{R}^{r}{E\,dr}\quad \ldots \ldots \ldots \ldots \ldots \left( 2 \right)$
1. Medan Listrik dan Potensial di dalam Bola Konduktor
Pada Gambar a, permukaan Gauss berada di dalam bola konduktor. Artinya tidak ada muatan yang dilingkupi (dibungkus) oleh permukaan Gauss $\left( Q=0 \right)$. Ingat bahwa muatan listrik bola konduktor tersebar hanya di permukaan bola, jadi tidak ada muatan di dalam bola konduktor. Jika nilai $Q=0$ dan agar persamaan 1 konsisten, maka nilai medan listrik harus nol $\left( E=0 \right)$.
Jadi dapat disimpulkan bahwa kuat medan listrik untuk titik di dalam bola konduktor $\left( r<R \right)$ pasti bernilai nol $\left( E=0 \right)$.
Berdasarkan hubungan persamaan 2, untuk $E=0$ maka nilai ${{V}_{r}}={{V}_{R}}$. Jadi nilai potensial listrik di dalam bola konduktor adalah:
$V=k\frac{Q}{R}\quad \ldots \ldots \ldots \ldots \ldots \left( 3 \right)$
2. Medan Listrik dan Potensial di permukaan Bola Konduktor
Pada Gambar b, permukaan Gauss berada tepat di permukaan bola konduktor. Artinya muatan yang dilingkupi (dibungkus) oleh permukaan Gauss adalah sebesar $Q$. Ingat bahwa muatan listrik bola konduktor tersebar hanya di permukaan bola, jadi tepat dilingkupi oleh bola konduktor. Berdasarkan kondisi fisis tersebut, maka persamaan 1 dapat dianalisis sebagai berikut.
$\int{E\,dA}=\frac{Q}{{{\varepsilon }_{o}}}$
$E\,A=\frac{Q}{{{\varepsilon }_{o}}}$
$E\,\left( 4\pi {{r}^{2}} \right)=\frac{Q}{{{\varepsilon }_{o}}}$ permukaan Gauss berbentuk bola, maka $A=4\pi {{r}^{2}}$.
$E\,=\frac{Q}{{{\varepsilon }_{o}}}\frac{1}{4\pi {{r}^{2}}}$
$E\,=\frac{1}{4\pi {{\varepsilon }_{o}}}\frac{Q}{{{r}^{2}}}$ dengan nilai $k=\frac{1}{4\pi {{\varepsilon }_{o}}}$ dan nilai $r=R$ (tepat di permukaan bola), maka:
$E=k\frac{Q}{{{R}^{2}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 4 \right)$
Potensial listrik di permukaan bola didapatkan berdasarkan integrasi persamaan 2, sehingga didapatkan persamaan berikut ini.
$V=k\frac{Q}{R}\quad \ldots \ldots \ldots \ldots \ldots \left( 5 \right)$
3. Medan Listrik dan Potensial di luar Bola Konduktor
Pada Gambar c, permukaan Gauss lebih luas dari pada permukaan bola konduktor. Artinya seluruh bola konduktor terlingkupi oleh permukaan Gauss. Oleh karena itu muatan yang dilingkupi (dibungkus) oleh permukaan Gauss adalah sebesar $Q$. Berdasarkan kondisi fisis tersebut, maka persamaan 1 dapat dianalisis dengan cara yang sama seperti kondisi di permukaan bola. Bedanya hanya nilai $r\ne R$ tetapi $r>R$. Sehingga persamaan untuk menentukan medan listrik pada titik yang berjarak $r$ dari pusat bola adalah:
$E=k\frac{Q}{{{r}^{2}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 6 \right)$
Berdasarkan integrasi persamaan 2, potensial listrik pada titik di luar bola konduktor seperti potensial yang dihasilkan muatan titik. Jadi bola dianggap sebagai muatan titik, sehingga persamaan potensial di luar bola konduktor adalah:
$V=k\frac{Q}{r}\quad \ldots \ldots \ldots \ldots \ldots \left( 7 \right)$
Agar lebih mudah dipahami, gambar di bawah ini memberikan ilustrasi nilai medan listrik dan potensial listrik untuk masing-masing area pada bola konduktor. Gambar a merupakan grafik besar medan listrik terhadap jarak titik dari pusat bola, sedangkan Gambar b merupakan grafik potensial listrik.
 |
| Ilustrasi Kuat Medan dan Potensial Listrik Bola Konduktor |
Contoh Soal Bola Konduktor
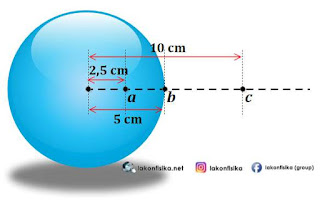
(1). Bola konduktor memiliki jari-jari $5\,cm$ dengan muatan total sebesar $20\,\mu C$ yang tersebar merata. Tentukan medan dan potensial listrik pada masing-masing titik berjarak: (a) $2,5\,cm$, (b) $5\,cm$, dan (c) $10\,cm$ dari pusat bola.
Jawab:
(a) titik berjarak $r=2,5\,cm$ dari pusat bola ($r<R$ atau di dalam bola)
$E=0$
$V=k\frac{Q}{R}$
$V=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{5\cdot {{10}^{-2}}}$
$V=3,6\cdot {{10}^{6}}\,volt$
(b) titik berjarak $r=5\,cm$ dari pusat bola ($r=R$ atau di permukaan bola)
$E=k\frac{Q}{{{R}^{2}}}$
$E=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{{{\left( 5\cdot {{10}^{-2}} \right)}^{2}}}$
$E=7,2\cdot {{10}^{7}}\,{N}/{C}\;$
$V=k\frac{Q}{R}$
$V=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{5\cdot {{10}^{-2}}}$
$V=3,6\cdot {{10}^{6}}\,volt$
(c) titik berjarak $r=10\,cm$ dari pusat bola ($r>R$ atau di luar bola)
$E=k\frac{Q}{{{r}^{2}}}$
$E=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{{{\left( 10\cdot {{10}^{-2}} \right)}^{2}}}$
$E=1,8\cdot {{10}^{7}}\,{N}/{C}\;$
$V=k\frac{Q}{r}$
$V=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{10\cdot {{10}^{-2}}}$
$V=1,8\cdot {{10}^{6}}\,volt$
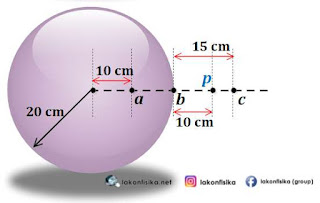
(2). Bola tipis berongga memiliki jari-jari 20 cm. Jika kuat medan listrik pada suatu titik di luar bola yang berjarak $10\,cm$ dari kulit bola adalah $8\times {{10}^{3}}\,{N}/{C}\;$, maka tentukan kuat medan listrik pada: (a) titik yang berjarak $10\,cm$ dari pusat bola, (b) kulit bola, dan (c) titik di luar bola yang berjarak $15\,cm$ dari kulit bola.
Jawab:
Berdasarkan kondisi awal ${{r}_{p}}=30\,cm$ dari pusat bola (titik P di luar bola), maka dapat ditentukan terlebih dahulu nilai muatan total:
$E=k\frac{Q}{r_{p}^{2}}$
$Q=E\frac{r_{p}^{2}}{k}$
$Q=8\cdot {{10}^{3}}\frac{{{\left( 3\cdot {{10}^{-1}} \right)}^{2}}}{9\cdot {{10}^{9}}}$
$Q=8\cdot {{10}^{-8}}\,C$
(a) titik a dengan ${{r}_{a}}=10\,cm$ dari pusat bola (${{r}_{a}}<R$ atau di dalam bola)
$E=0$
(b) titik a dengan ${{r}_{b}}=20\,cm$ dari pusat bola (${{r}_{b}}=R$ atau di permukaan bola)
$E=k\frac{Q}{{{R}^{2}}}$
$E=9\cdot {{10}^{9}}\frac{8\cdot {{10}^{-8}}}{{{\left( 2\cdot {{10}^{-1}} \right)}^{2}}}$
$E=1,8\cdot {{10}^{4}}\,{N}/{C}\;$
(c) titik a dengan ${{r}_{c}}=35\,cm$ dari pusat bola (${{r}_{c}}>R$ atau di luar bola)
$E=k\frac{Q}{{{r}_{c}}^{2}}$
$E=9\cdot {{10}^{9}}\frac{8\cdot {{10}^{-8}}}{{{\left( 3,5\cdot {{10}^{-1}} \right)}^{2}}}$
$E=5,9\cdot {{10}^{3}}\,{N}/{C}\;$