Konsep dan Contoh Soal Besaran Vektor – Resultan Vektor - Fisika SMA Kelas 10
Jul 7, 2019
Edit
Beberapa besaran dalam fisika tidak cukup dinyatakan dengan nilai saja, tetapi juga memerlukan arah. Jenis besaran yang mempunyai nilai dan arah disebut sebagai besaran vektor. Pemahaman vektor sangat diperlukan sebagai modal dasar untuk memahami topik-topik fisika lainnya. Oleh karena itu, pada materi fisika SMA kelas 10 selalu didahului dengan konsep besaran dan satuan, selanjutnya dipelajari besaran vektor secara khusus. Beberapa topik yang perlu dipahami tentang besaran vektor di SMA Kelas 10 adalah:
a. konsep sistem koordinat kartesius
b. cara penguraian vektor, yang tentunya membutuhkan pemahaman konsep trigonometri dasar (sin, cos, tan)
c. cara mencari resultan vektor
Secara geometri, besaran vektor dinyatakan dalam gambar panah seperti di bawah. Besar nilai vektor $\overrightarrow{\text{A}}$ diilustrasikan dengan panjang anak panah, semakin panjang anak panah, maka semakin besar nilai besaran vektor itu. Sedangkan arah vektor $\overrightarrow{\text{A}}$ ditunjukkan dengan ujung mata panah.
Sebelum lanjut ke proses analisis vektor, kita pahami bersama tentang konsep dasar trigonometri. Secara sederhana, trigonometri membahas tentang perbandingan sisi-sisi segitiga siku-siku. Ilustrasinya seperti gambar di bawah ini.
Gambar di atas merupakan segitiga siku-siku dengan salah satu sudutnya sebesar $\alpha $. Sisi $y$ berada di depan sudut $\alpha $, sisi $x$ berada di kaki sudut atau di samping sudut $\alpha $, dan $r$ merupakan sisi iring segitiga siku-siku. Trigonometri secara sederhana dapat dinyatakan sebagai unsur perbandingan antara sisi-sisi dalam segitiga siku-siku. Ada 3 unsur dasar perbandingan sisi dalam trigonometri, yaitu sinus $\left( \sin \right)$, cosinus $\left( \cos \right)$, dan tangen $\left( \tan \right)$. Jika kita ingin menentukan unsur-unsur dasar trigonometri dari sudut $\alpha $, maka berikut ini persamaannya:
$\begin{align} & \sin \alpha =\frac{y}{r}\quad \frac{\text{(sisi depan)}}{\text{(sisi miring)}}\quad \to y=r\sin \alpha \quad \to r=\frac{y}{\sin \alpha } \\ & \cos \alpha =\frac{x}{r}\quad \frac{\text{(sisi samping)}}{\text{(sisi miring)}}\quad \to x=r\cos \alpha \quad \to r=\frac{x}{\cos \alpha } \\ & \tan \alpha =\frac{y}{x}\quad \frac{\text{(sisi depan)}}{\text{(sisi samping)}}\quad \to y=x\tan \alpha \quad \to x=\frac{y}{\tan \alpha } \\ \end{align}$
Gambar di atas memberikan ilustrasi hasil penguraian vektor $\overrightarrow{\text{A}}$ menjadi komponennya di sumbu x $\left( \overrightarrow{{{\text{A}}_{x}}} \right)$ dan komponennya di sumbu y $\left( \overrightarrow{{{\text{A}}_{y}}} \right)$. Arah vektor $\overrightarrow{\text{A}}$ membentuk sudut $\alpha $ terhadap sumbu x positif. Cara menentukan komponen vektor di sumbu x adalah dengan menarik garis tegak lurus sumbu x dari ujung vektor $\overrightarrow{\text{A}}$ sampai memotong sumbu x. Selanjutnya ditarik anak panah dari pangkal vektor $\overrightarrow{\text{A}}$ sampai titik potong tersebut, maka diperoleh vektor $\overrightarrow{{{\text{A}}_{x}}}$. Sedangkan untuk menentukan komponen vektor di sumbu y adalah dengan menarik garis tegak lurus sumbu y dari ujung vektor $\overrightarrow{\text{A}}$ sampai memotong sumbu y. Selanjutnya ditarik anak panah dari pangkal vektor $\overrightarrow{\text{A}}$ sampai titik potong tersebut, maka diperoleh vektor $\overrightarrow{{{\text{A}}_{y}}}$.
Jika diperhatikan luasan segitiga yang diarsir, maka kita bisa menentukan besar masing-masing komponen vektor berdasarkan konsep trigonometri. Panjang vektor $\overrightarrow{\text{A}}$ sebagai sisi miring, $\overrightarrow{{{\text{A}}_{x}}}$ sebagai sisi samping sudut $\alpha $, dan $\overrightarrow{{{\text{A}}_{y}}}$ sama dengan sisi depan sudut $\alpha $.
$\begin{align}
& \overrightarrow{A}={{A}_{x}}\widehat{i}+{{A}_{y}}\widehat{j} \\
& \overrightarrow{A}=\left( A\cos \alpha \right)\widehat{i}+\left( A\sin \alpha \right)\widehat{j} \\
\end{align}$
c. setelah diuraikan, maka vektor $\overrightarrow{A}$ sudah “hilang” dan diganti komponen $\overrightarrow{{{A}_{x}}}$ dan $\overrightarrow{{{A}_{y}}}$, begitu pula vektor $\overrightarrow{B}$ “hilang” dan diganti $\overrightarrow{{{B}_{x}}}$ dan $\overrightarrow{{{B}_{y}}}$, sedangkan vektor $\overrightarrow{C}$ tetap ada karena tidak diuraikan (sudah berada di sumbu y)
d. jumlahkan seluruh komponen vektor pada masing-masing sumbu koordinat:
\[\begin{align}
& \sum{{{R}_{x}}}={{A}_{x}}-{{B}_{x}} \\
& {{B}_{x}}\text{ bertanda (-) karena arahnya ke sumbu x (-)} \\
& \sum{{{R}_{y}}}={{A}_{y}}+{{B}_{y}}-C \\
& C\text{ bertanda (-) karena arahnya ke sumbu y (-)} \\
\end{align}\]
e. tentukan nilai atau besar resultannya:
\[R=\sqrt{{{\left( \sum{{{R}_{x}}} \right)}^{2}}+{{\left( \sum{{{R}_{y}}} \right)}^{2}}}\text{ dengan arah: }\theta ={{\tan }^{-1}}\left( \frac{\sum{{{R}_{y}}}}{\sum{{{R}_{x}}}} \right)\]
Nilai ${{R}_{x}}=2$ dan ${{R}_{y}}=-4$
Besar Resultan adalah:
$\begin{align} & R=\sqrt{R_{x}^{2}+R_{y}^{2}} \\ & R=\sqrt{{{2}^{2}}+{{\left( -4 \right)}^{2}}} \\ & R=\sqrt{20}=2\sqrt{5}\ m \\ \end{align}$
Arah perpindahan:
$\begin{align} & \tan \theta =\frac{{{R}_{x}}}{{{R}_{y}}} \\ & \tan \theta =\frac{-2}{4} \\ & \tan \theta =\frac{-1}{2}\to \text{ada di kuadran IV, sehingga }\theta ={{\tan }^{-1}}\left( \frac{-1}{2} \right)\approx {{333}^{o}} \\ \end{align}$
Jadi besar resultan perpindahan adalah $R=2\sqrt{5}\ m$ dengan arah $\theta \approx {{333}^{o}}$ dari sumbu x positif.
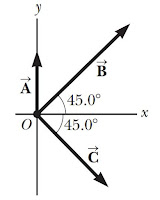
(2). Tiga vektor perpindahan masing-masing sebesar $\left| \overrightarrow{A} \right|=2\sqrt{2}\ m$, $\left| \overrightarrow{B} \right|=6\ m$, dan $\left| \overrightarrow{C} \right|=4\ m$ dengan arah seperti gambar di bawah. Tentukan besar resultan dan arah perpindahan ketiga vektor tersebut!
Untuk lebih memahami konsep vektor, silakan dipelajari bersama contoh soal vektor berikut:
Soal Vektor UN Fisika SMA
Soal HOTS Fisika Vektor
a. konsep sistem koordinat kartesius
b. cara penguraian vektor, yang tentunya membutuhkan pemahaman konsep trigonometri dasar (sin, cos, tan)
c. cara mencari resultan vektor
Secara geometri, besaran vektor dinyatakan dalam gambar panah seperti di bawah. Besar nilai vektor $\overrightarrow{\text{A}}$ diilustrasikan dengan panjang anak panah, semakin panjang anak panah, maka semakin besar nilai besaran vektor itu. Sedangkan arah vektor $\overrightarrow{\text{A}}$ ditunjukkan dengan ujung mata panah.
 |
| Gambar Komponen-Komponen Vektor |
1. Cara Penguraian Vektor (Analisis Komponen Vektor dan Vektor Satuan)
Analisis vektor dapat dilakukan dengan cara menguraikan menjadi komponen-komponen penyusunnya. Syarat utama untuk melakukan analisis vektor adalah memahami sistem koordinat dan konsep dasar trigonometri. Sistem koordinat menjadi dasar penguraian vektor karena dalam proses analisisnya, vektor ditempatkan dalam koordinat dan diuraikan ke masing-masing sumbu koordinat. Notasi vektor juga dapat ditulis dalam vektor satuan, dengan masing-masing vektor satuan di sumbu x adalah $\widehat{i}$, sumbu y adalah $\widehat{j}$, dan sumbu z adalah $\widehat{k}$.Sebelum lanjut ke proses analisis vektor, kita pahami bersama tentang konsep dasar trigonometri. Secara sederhana, trigonometri membahas tentang perbandingan sisi-sisi segitiga siku-siku. Ilustrasinya seperti gambar di bawah ini.
 |
| Gambar Perbandingan Sisi-Sisi Segitiga Siku-Siku |
Gambar di atas merupakan segitiga siku-siku dengan salah satu sudutnya sebesar $\alpha $. Sisi $y$ berada di depan sudut $\alpha $, sisi $x$ berada di kaki sudut atau di samping sudut $\alpha $, dan $r$ merupakan sisi iring segitiga siku-siku. Trigonometri secara sederhana dapat dinyatakan sebagai unsur perbandingan antara sisi-sisi dalam segitiga siku-siku. Ada 3 unsur dasar perbandingan sisi dalam trigonometri, yaitu sinus $\left( \sin \right)$, cosinus $\left( \cos \right)$, dan tangen $\left( \tan \right)$. Jika kita ingin menentukan unsur-unsur dasar trigonometri dari sudut $\alpha $, maka berikut ini persamaannya:
$\begin{align} & \sin \alpha =\frac{y}{r}\quad \frac{\text{(sisi depan)}}{\text{(sisi miring)}}\quad \to y=r\sin \alpha \quad \to r=\frac{y}{\sin \alpha } \\ & \cos \alpha =\frac{x}{r}\quad \frac{\text{(sisi samping)}}{\text{(sisi miring)}}\quad \to x=r\cos \alpha \quad \to r=\frac{x}{\cos \alpha } \\ & \tan \alpha =\frac{y}{x}\quad \frac{\text{(sisi depan)}}{\text{(sisi samping)}}\quad \to y=x\tan \alpha \quad \to x=\frac{y}{\tan \alpha } \\ \end{align}$
 |
| Gambar Cara Penguraian Vektor |
Gambar di atas memberikan ilustrasi hasil penguraian vektor $\overrightarrow{\text{A}}$ menjadi komponennya di sumbu x $\left( \overrightarrow{{{\text{A}}_{x}}} \right)$ dan komponennya di sumbu y $\left( \overrightarrow{{{\text{A}}_{y}}} \right)$. Arah vektor $\overrightarrow{\text{A}}$ membentuk sudut $\alpha $ terhadap sumbu x positif. Cara menentukan komponen vektor di sumbu x adalah dengan menarik garis tegak lurus sumbu x dari ujung vektor $\overrightarrow{\text{A}}$ sampai memotong sumbu x. Selanjutnya ditarik anak panah dari pangkal vektor $\overrightarrow{\text{A}}$ sampai titik potong tersebut, maka diperoleh vektor $\overrightarrow{{{\text{A}}_{x}}}$. Sedangkan untuk menentukan komponen vektor di sumbu y adalah dengan menarik garis tegak lurus sumbu y dari ujung vektor $\overrightarrow{\text{A}}$ sampai memotong sumbu y. Selanjutnya ditarik anak panah dari pangkal vektor $\overrightarrow{\text{A}}$ sampai titik potong tersebut, maka diperoleh vektor $\overrightarrow{{{\text{A}}_{y}}}$.
Jika diperhatikan luasan segitiga yang diarsir, maka kita bisa menentukan besar masing-masing komponen vektor berdasarkan konsep trigonometri. Panjang vektor $\overrightarrow{\text{A}}$ sebagai sisi miring, $\overrightarrow{{{\text{A}}_{x}}}$ sebagai sisi samping sudut $\alpha $, dan $\overrightarrow{{{\text{A}}_{y}}}$ sama dengan sisi depan sudut $\alpha $.
\[\begin{align}
& \sin \alpha =\frac{{{\text{A}}_{y}}}{\text{A}}\quad \text{, maka nilai:}\quad {{\text{A}}_{y}}=\text{A}\sin \alpha \\
& \text{dan} \\
& \cos \alpha =\frac{{{\text{A}}_{x}}}{\text{A}}\quad \text{, maka nilai:}\quad {{\text{A}}_{x}}=\text{A}cos\alpha \\
\end{align}\]
Berdasarkan hasil penguraian vektor menjadi komponen-komponennya, maka vektor 2 dimensi (sumbu x dan y) dapat dituliskan dengan notasi:
2. Resultan Vektor dengan Metode Jajar Genjang
Metode jajar genjang secara umum digunakan untuk menentukan resultan 2 vektor. Jika ada lebih dari 2 vektor, maka metode ini akan lebih sulit digunakan. Seperti namanya, metode ini menggunakan bentuk bangun jajar genjang untuk menentukan resultan 2 vektor.
Jika ada vektor $\overrightarrow{a}$ dan vektor $\overrightarrow{b}$ yang saling mengapit sudut $\alpha $, maka dapat ditentukan resultan vektor $\overrightarrow{R}$ seperti gambar di atas. Vektor $\overrightarrow{R}$ diperoleh dengan melengkapkan bentuk jajar genjang melalui garis bantu putus-putus sehingga membentuk jajar genjang. Selanjutnya dari pangkal kedua vektor ditarik anak panah menuju titik potong garis putus-putus tadi.
Resultan vektor merupakan hasil penjumlahan atau pengurangan vektor. Jika $\overrightarrow{R}$ merupakan hasil penjumlahan $\left( \overrightarrow{R}=\overrightarrow{a}+\overrightarrow{b} \right)$, maka masing-masing vektor $\overrightarrow{a}$ dan $\overrightarrow{b}$ tidak perlu diubah arahnya saat menggambarkan resultan. Tetapi jika $\overrightarrow{R}$ merupakan hasil pengurangan $\left( \overrightarrow{R}=\overrightarrow{a}-\overrightarrow{b} \right)$, maka arah vektor $\overrightarrow{b}$ perlu dibalik karena menjadi bertanda negatif.
Sedangkan nilai vektor $\overrightarrow{R}$ untuk masing-masing hasil penjumlahan dan pengurangan vektor dapat dihitung dengan persamaan 1 di bawah ini.
$R=\left| \overrightarrow{a} \right|\pm \left| \overrightarrow{b} \right|=\sqrt{{{a}^{2}}+{{b}^{2}}\pm 2\cdot a\cdot b\cos \alpha }\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
3. Resultan Vektor dengan Metode Analisis Komponen
Metode analisis vektor dapat digunakan sebagai cara untuk menentukan resultan vektor. Kelebihan metode ini adalah dapat dengan mudah menentukan resultan lebih dari 2 vektor sekaligus. Tetapi metode ini menuntut kemampuan analisis yang teliti dan telaten. Pada dasarnya, metode ini dilakukan dengan menguraikan seluruh vektor menjadi komponen-komponen di sumbu koordinat (kalau 2 dimensi ada sumbu x dan y). Selanjutnya mencari jumlah seluruh komponen vektor di masing-masing sumbu koordinat, dan mencari resultan dari masing-masing jumlahnya. Untuk lebih jelasnya, kita pahami bersama ilustrasi cara mencari resultan 3 vektor pada gambar di bawah ini.
Pada gambar di atas ada 3 vektor masing-masing adalah $\overrightarrow{A}$, $\overrightarrow{B}$, dan $\overrightarrow{C}$. Untuk mencari resultan 3 vektor tersebut, berikut ini langkahnya:
a. tempatkan masing-masing pangkal vektor pada pusat koordinat
b. uraikan masing-masing komponen vektor pada sumbu x dan y, jika ada vektor yang sudah sejajar (berada dalam sumbu koordinat tertentu) maka tidak perlu diuraikan lagi, contohnya adalah vektor $\overrightarrow{C}$
c. setelah diuraikan, maka vektor $\overrightarrow{A}$ sudah “hilang” dan diganti komponen $\overrightarrow{{{A}_{x}}}$ dan $\overrightarrow{{{A}_{y}}}$, begitu pula vektor $\overrightarrow{B}$ “hilang” dan diganti $\overrightarrow{{{B}_{x}}}$ dan $\overrightarrow{{{B}_{y}}}$, sedangkan vektor $\overrightarrow{C}$ tetap ada karena tidak diuraikan (sudah berada di sumbu y)
d. jumlahkan seluruh komponen vektor pada masing-masing sumbu koordinat:
e. tentukan nilai atau besar resultannya:
\[R=\sqrt{{{\left( \sum{{{R}_{x}}} \right)}^{2}}+{{\left( \sum{{{R}_{y}}} \right)}^{2}}}\text{ dengan arah: }\theta ={{\tan }^{-1}}\left( \frac{\sum{{{R}_{y}}}}{\sum{{{R}_{x}}}} \right)\]
Contoh Soal Analisis Resultan Vektor
(1). Tentukan resultan dua vektor perpindahan dan dari gerak seorang anak dalam bidang x dan y!
Jawab:
$\begin{align} & \overrightarrow{R}=\overrightarrow{A}+\overrightarrow{B} \\ & \overrightarrow{R}=\left( 2\widehat{i}+2\widehat{j} \right)+\left( 2\widehat{i}-4\widehat{j} \right) \\ & \overrightarrow{R}=\left( 2+2 \right)\widehat{i}+\left( 2-4 \right)\widehat{j} \\ & \overrightarrow{R}=4\widehat{i}+\left( -2\widehat{j} \right) \\ \end{align}$Nilai ${{R}_{x}}=2$ dan ${{R}_{y}}=-4$
Besar Resultan adalah:
$\begin{align} & R=\sqrt{R_{x}^{2}+R_{y}^{2}} \\ & R=\sqrt{{{2}^{2}}+{{\left( -4 \right)}^{2}}} \\ & R=\sqrt{20}=2\sqrt{5}\ m \\ \end{align}$
Arah perpindahan:
$\begin{align} & \tan \theta =\frac{{{R}_{x}}}{{{R}_{y}}} \\ & \tan \theta =\frac{-2}{4} \\ & \tan \theta =\frac{-1}{2}\to \text{ada di kuadran IV, sehingga }\theta ={{\tan }^{-1}}\left( \frac{-1}{2} \right)\approx {{333}^{o}} \\ \end{align}$
Jadi besar resultan perpindahan adalah $R=2\sqrt{5}\ m$ dengan arah $\theta \approx {{333}^{o}}$ dari sumbu x positif.
Jawab:
$\begin{align} & \sum{{{R}_{x}}}={{B}_{x}}+{{C}_{x}} \\ & \sum{{{R}_{x}}}=B\cos {{45}^{\circ }}+C\cos {{45}^{\circ }} \\ & \sum{{{R}_{x}}}=6\cdot \frac{1}{2}\sqrt{2}+4\cdot \frac{1}{2}\sqrt{2} \\ & \sum{{{R}_{x}}}=5\sqrt{2}\ m \\ \end{align}$
dan
$\begin{align} & \sum{{{R}_{y}}}={{B}_{y}}+A-{{C}_{y}} \\ & \sum{{{R}_{y}}}=B\sin {{45}^{\circ }}+A-C\sin {{45}^{\circ }} \\ & \sum{{{R}_{y}}}=6\cdot \frac{1}{2}\sqrt{2}+2\sqrt{2}-4\cdot \frac{1}{2}\sqrt{2} \\ & \sum{{{R}_{y}}}=3\sqrt{2}\ m \\ \end{align}$
Resultan ketiga vektor adalah:
$\begin{align} & R=\sqrt{{{\left( \sum{{{R}_{x}}} \right)}^{2}}+{{\left( \sum{{{R}_{y}}} \right)}^{2}}} \\ & R=\sqrt{{{\left( 5\sqrt{2} \right)}^{2}}+{{\left( 3\sqrt{2} \right)}^{2}}} \\ & R=\sqrt{50+18} \\ & R=\sqrt{68}=2\sqrt{17}\ m \\ \end{align}$
dengan arah
$\begin{align} & \theta ={{\tan }^{-1}}\left( \frac{3\sqrt{2}}{5\sqrt{2}} \right) \\ & \theta ={{\tan }^{-1}}\left( \frac{3}{5} \right)\text{ (ada di kuadran I)} \\ & \theta ={{37}^{\circ }} \\ \end{align}$
Jadi besar resultan vektor perpindahan adalah $R=2\sqrt{17}\ m$ dengan arah $\theta ={{37}^{\circ }}$ terhadap sumbu x positif
$\begin{align} & \sum{{{R}_{x}}}={{B}_{x}}+{{C}_{x}} \\ & \sum{{{R}_{x}}}=B\cos {{45}^{\circ }}+C\cos {{45}^{\circ }} \\ & \sum{{{R}_{x}}}=6\cdot \frac{1}{2}\sqrt{2}+4\cdot \frac{1}{2}\sqrt{2} \\ & \sum{{{R}_{x}}}=5\sqrt{2}\ m \\ \end{align}$
dan
$\begin{align} & \sum{{{R}_{y}}}={{B}_{y}}+A-{{C}_{y}} \\ & \sum{{{R}_{y}}}=B\sin {{45}^{\circ }}+A-C\sin {{45}^{\circ }} \\ & \sum{{{R}_{y}}}=6\cdot \frac{1}{2}\sqrt{2}+2\sqrt{2}-4\cdot \frac{1}{2}\sqrt{2} \\ & \sum{{{R}_{y}}}=3\sqrt{2}\ m \\ \end{align}$
Resultan ketiga vektor adalah:
$\begin{align} & R=\sqrt{{{\left( \sum{{{R}_{x}}} \right)}^{2}}+{{\left( \sum{{{R}_{y}}} \right)}^{2}}} \\ & R=\sqrt{{{\left( 5\sqrt{2} \right)}^{2}}+{{\left( 3\sqrt{2} \right)}^{2}}} \\ & R=\sqrt{50+18} \\ & R=\sqrt{68}=2\sqrt{17}\ m \\ \end{align}$
dengan arah
$\begin{align} & \theta ={{\tan }^{-1}}\left( \frac{3\sqrt{2}}{5\sqrt{2}} \right) \\ & \theta ={{\tan }^{-1}}\left( \frac{3}{5} \right)\text{ (ada di kuadran I)} \\ & \theta ={{37}^{\circ }} \\ \end{align}$
Jadi besar resultan vektor perpindahan adalah $R=2\sqrt{17}\ m$ dengan arah $\theta ={{37}^{\circ }}$ terhadap sumbu x positif
Untuk lebih memahami konsep vektor, silakan dipelajari bersama contoh soal vektor berikut:
Soal Vektor UN Fisika SMA
Soal HOTS Fisika Vektor