Konsep dan Contoh Soal Fluida Statis – Hukum Archimedes - Fisika SMA Kelas 11
Jun 29, 2019
Edit
Secara sederhana, fluida dapat didefinisikan sebagai fase zat (wujud zat) yang memiliki sifat dapat mengalir, mudah berubah bentuk (mengikuti bentuk ruang), dan secara atomik memiliki ikatan atom yang lemah. Gas dan cair merupakan wujud zat yang termasuk dalam kategori fluida. Karena fluida merupakan bagian terbesar dalam alam ini dan berperan penting dalam siklus alam, maka beberapa cabang ilmu terapan juga mengkaji fluida secara mendalam, contohnya adalah tentang mekanika fluida.
Dalam mekanika fluida, dibahas tentang kinematika fluida (aliran fluida) dan dinamika fluida (aspek gaya, tekanan, energi dalam fluida). Dalam materi fisika SMA kelas 11, dibahas secara khusus konsep dasar fluida, yang dibagi menjadi fluida statis dan fluida dinamis. Nah, kali ini kita akan belajar bersama tentang konsep fluida statis (fluida tak mengalir) yang terbagi menjadi beberapa topik, yaitu konsep tekanan (Hukum Pascal), tekanan hidrostatis, dan Hukum Archimedes. Model soal fluida statis sangat variatif, karena bisa dikombinasikan juga dengan konsep dinamika Hukum Newton. Jadi sangat dimungkinkan muncul soal HOTS fisika tentang fluida statis dalam ujian atau tes di tingkat SMA (UN SMA, UTBK SBMPTN, SIMAK UI, atau UTUL UGM). Sekarang langsung saja kita simak bersama Konsep dan Contoh Soal Fluida Statis, tekanan hidrostatis, Hukum Pascal, dan Hukum Archimedes untuk materi Fisika SMA Kelas 11.
$p=\frac{F}{A}...................\left( 1 \right)$
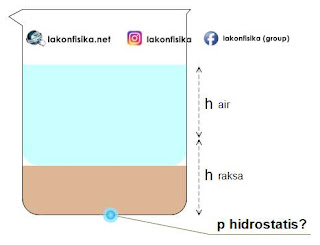
Tekanan menjadi suatu besaran yang sangat penting dalam melakukan analisis sistem fluida. Berdasarkan hasil observasi yang telah dilakukan, fluida memberikan tekanan ke segala arah. Contohnya adalah pada gambar di atas. Jika ada suatu benda berada di dalam fluida, maka benda tersebut akan mendapatkan tekanan fluida dari segala arah. Besar tekanan dari satu arah pasti nilainya sama dengan tekanan dari arah yang berlawanan. Tekanan di dalam fluida cair yang diam juga disebut sebagai tekanan hidrostatis.
Sekarang coba kita tentukan berapa nilai tekanan hidrostatis pada kedalaman $h$ dari permukaan zat cair seperti gambar di atas. Tekanan hidrostatis pada kedalaman $h$ bergantung pada gaya berat zat cair yang berada di atasnya.
Berat zat cair adalah
$w=m\ g=\left( \rho \ V \right)g$, dengan nilai $m=\rho \ V$
$w=\rho \left( Ah \right)g$, dengan nilai $V=A\ h$
Selanjutnya nilai tekanan adalah
$\begin{align}
& p=\frac{w}{A} \\
& p=\frac{\rho \ A\ h\ g}{A} \\
& p=\rho \ h\ g....................\left( 2 \right) \\
\end{align}$
Berdasarkan cara memperoleh persamaan 2 di atas, komponen $A$ (luas penampang) dapat dieliminasi. Secara matematis hal ini berarti bahwa nilai tekanan pada kedalaman $h$ tidak dipengaruhi oleh luas penampang zat cair. Artinya, seluruh titik pada kedalaman $h$ mendapatkan tekanan hidrostatis yang sama. Jadi tekanan hidrostatis pada suatu zat cair pada kondisi yang sama hanya dipengaruhi oleh posisi kedalaman. Jika diminta menentukan perbedaan tekanan $\Delta p$ dari dua titik yang berbeda kedalamannya, maka cukup kita perhatikan perbedaan kedalamannya $\Delta h$ saja.
Dalam sistem pompa hidrolik di atas, fluida berbentuk bejana berhubungan dengan sistem input dan output dengan luas penampang yang berbeda. Sesuai dengan prinsip Pascal, jika fluida tersebut diberikan tekanan input ${{p}_{in}}$, dengan gaya ${{F}_{in}}$, maka tekanan tersebut akan diteruskan ke penampang output $\left( {{A}_{out}} \right)$dengan besar tekanan yang sama $\left( {{p}_{in}}={{p}_{out}} \right)$. Sehingga pada penampang output akan menghasilkan gaya output ${{F}_{out}}$. Konsep tersebut jika dinyatakan dalam bentuk matematik adalah sebagai berikut:
$\begin{align}
& {{p}_{in}}={{p}_{out}} \\
& \frac{{{F}_{in}}}{{{A}_{in}}}=\frac{{{F}_{out}}}{{{A}_{out}}}\ldots \ldots \ldots \ldots \ldots \left( 3 \right) \\
\end{align}$
Berdasarkan persamaan 3 di atas, kita dapat menyatakan bahwa gaya berbanding lurus dengan luas penampang. Jika ${{F}_{in}}$ yang kecil diberikan pada penampang input ${{A}_{in}}$ yang kecil pula, maka akan menghasilkan ${{F}_{out}}$ yang besar pada penampang output ${{A}_{out}}$ yang lebih besar. Nah, dari konsep tersebut pompa hidrolik dimanfaatkan untuk mengangkat beban yang besar hanya dengan gaya kecil. Perbandingan $\frac{{{F}_{out}}}{{{F}_{in}}}$ disebut sebagai keuntungan mekanik.
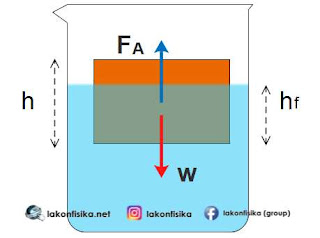
Penampang atas benda yang berada pada kedalaman ${{h}_{1}}$ mendapatkan tekanan sebesar ${{p}_{1}}$ sehingga ada gaya ${{F}_{1}}$ ke arah bawah terhadap penampang atas benda. Begitu pula terjadi pada penampang benda bagian bawah. Pada penampang bawah benda yang berada di kedalaman ${{h}_{2}}$, fluida memberikan tekanan hidrostatis sebesar ${{p}_{2}}$ sehingga benda mendapatkan gaya ${{F}_{2}}$ ke atas. Nah, selisih antara ${{F}_{2}}$ dan ${{F}_{1}}$ merupakan gaya apung fluida ${{F}_{A}}$ yang diberikan pada benda. Secara matematis, konsep tersebut dijelaskan sebagai berikut:
$\begin{align}
& {{F}_{A}}={{F}_{2}}-{{F}_{1}} \\
& {{F}_{A}}={{p}_{2}}-{{p}_{1}} \\
& {{F}_{A}}=\left( {{\rho }_{f}}\ g\ {{h}_{2}} \right)A-\left( {{\rho }_{f}}\ g\ {{h}_{1}} \right)A \\
& {{F}_{A}}={{\rho }_{f}}\ g\ A\left( {{h}_{2}}-{{h}_{1}} \right) \\
& {{F}_{A}}={{\rho }_{f}}\ V\ g\ \ldots \ldots \ldots \ldots \ldots \left( 4 \right) \\
\end{align}$
Persamaan 4 merupakan besar gaya apung ${{F}_{A}}$ yang diberikan oleh fluida bermassa jenis ${{\rho }_{f}}$ kepada benda. Nah karena nilai ${{\rho }_{f}}\ V={{m}_{f}}$ yang merupakan massa fluida, maka:
$\begin{align}
& {{F}_{A}}={{\rho }_{f}}\ V\ g \\
& {{F}_{A}}={{m}_{f}}\ g \\
& {{F}_{A}}={{w}_{f}}\ \ldots \ldots \ldots \ldots \ldots \left( 5 \right) \\
\end{align}$
Berdasarkan persamaan 5, dapat disimpulkan bahwa besar gaya apung ${{F}_{A}}$ sama dengan berat fluida ${{w}_{f}}$ (bisa zat cair atau gas) yang dipindahkan akibat masuknya benda ke dalam fluida. Artinya, jumlah volume fluida yang dipindahkan $\left( V \right)$ sama dengan volume benda yang tercelup di dalam fluida. Konsep ini dinyatakan oleh ilmuan yang bernama Archimedes, dan disebut sebagai Hukum Archimedes.
(2). Sebuah kubus terbuat dari kayu mempunyai sisi 10 cm dan mengapung di atas permukaan cairan. Jika massa jenis cairan 1,2 g/cm3. Hitunglah
a) Tinggi kubus yang berada di bawah permukaan cairan jika massa jenis kayu 0,8 g/cm3
b) Besar gaya ke atas yang di alami kubus kayu tersebut
Dalam mekanika fluida, dibahas tentang kinematika fluida (aliran fluida) dan dinamika fluida (aspek gaya, tekanan, energi dalam fluida). Dalam materi fisika SMA kelas 11, dibahas secara khusus konsep dasar fluida, yang dibagi menjadi fluida statis dan fluida dinamis. Nah, kali ini kita akan belajar bersama tentang konsep fluida statis (fluida tak mengalir) yang terbagi menjadi beberapa topik, yaitu konsep tekanan (Hukum Pascal), tekanan hidrostatis, dan Hukum Archimedes. Model soal fluida statis sangat variatif, karena bisa dikombinasikan juga dengan konsep dinamika Hukum Newton. Jadi sangat dimungkinkan muncul soal HOTS fisika tentang fluida statis dalam ujian atau tes di tingkat SMA (UN SMA, UTBK SBMPTN, SIMAK UI, atau UTUL UGM). Sekarang langsung saja kita simak bersama Konsep dan Contoh Soal Fluida Statis, tekanan hidrostatis, Hukum Pascal, dan Hukum Archimedes untuk materi Fisika SMA Kelas 11.
1. Konsep Tekanan Hidrostatis
Tekanan dan gaya di dalam fluida saling berhubungan. Tekanan $p$ didefinisikan sebagai gaya $F$ tiap satuan luas $A$, dengan gaya bekerja secara tegak lurus terhadap luas penampang. Walaupun gaya merupakan besaran vektor, tekanan merupakan besaran skalar, yang hanya memiliki nilai saja. Dalam sistem satuan internasional, tekanan memiliki satuan $Pa$ (Pascal) atau ${N}/{{{m}^{2}}}\;$ dengan nilai $1 Pa=1 {N}/{{{m}^{2}}}\;$. Persamaan tekanan dapat dinyatakan sebagai berikut:$p=\frac{F}{A}...................\left( 1 \right)$
Tekanan menjadi suatu besaran yang sangat penting dalam melakukan analisis sistem fluida. Berdasarkan hasil observasi yang telah dilakukan, fluida memberikan tekanan ke segala arah. Contohnya adalah pada gambar di atas. Jika ada suatu benda berada di dalam fluida, maka benda tersebut akan mendapatkan tekanan fluida dari segala arah. Besar tekanan dari satu arah pasti nilainya sama dengan tekanan dari arah yang berlawanan. Tekanan di dalam fluida cair yang diam juga disebut sebagai tekanan hidrostatis.
Sekarang coba kita tentukan berapa nilai tekanan hidrostatis pada kedalaman $h$ dari permukaan zat cair seperti gambar di atas. Tekanan hidrostatis pada kedalaman $h$ bergantung pada gaya berat zat cair yang berada di atasnya.
Berat zat cair adalah
$w=m\ g=\left( \rho \ V \right)g$, dengan nilai $m=\rho \ V$
$w=\rho \left( Ah \right)g$, dengan nilai $V=A\ h$
Selanjutnya nilai tekanan adalah
$\begin{align}
& p=\frac{w}{A} \\
& p=\frac{\rho \ A\ h\ g}{A} \\
& p=\rho \ h\ g....................\left( 2 \right) \\
\end{align}$
Berdasarkan cara memperoleh persamaan 2 di atas, komponen $A$ (luas penampang) dapat dieliminasi. Secara matematis hal ini berarti bahwa nilai tekanan pada kedalaman $h$ tidak dipengaruhi oleh luas penampang zat cair. Artinya, seluruh titik pada kedalaman $h$ mendapatkan tekanan hidrostatis yang sama. Jadi tekanan hidrostatis pada suatu zat cair pada kondisi yang sama hanya dipengaruhi oleh posisi kedalaman. Jika diminta menentukan perbedaan tekanan $\Delta p$ dari dua titik yang berbeda kedalamannya, maka cukup kita perhatikan perbedaan kedalamannya $\Delta h$ saja.
Contoh Soal Tekanan Hidrostatis
Sebuah tabung yang luas penampangnya 10 cm2, diisi air raksa setinggi 10 cm dan air setinggi 50 cm dari permukaan raksa. Jika massa jenis air raksa 13,6 gr/cm3, massa jenis air 1 gr/cm3. Hitunglah tekanan hidrostatis dan gaya hidrostatis pada dasar tabung!
Jawab:
$\begin{align}
& A=10\ c{{m}^{2}}={{10}^{-3}}{{m}^{2}} \\
& {{h}_{r}}=10\ cm=0,1\ m \\
& {{h}_{a}}=50\ cm=0,5\ m \\
& {{\rho }_{a}}=1{gr}/{c{{m}^{3}}}\;=1{000\ kg}/{{{m}^{3}}}\; \\
& {{\rho }_{r}}=13,6{gr}/{c{{m}^{3}}}\;=13{600\ kg}/{{{m}^{3}}}\; \\
\end{align}$
$\begin{align}
& {{p}_{r}}={{\rho }_{r}}\,g\,{{h}_{r}} \\
& {{p}_{r}}=13600\cdot 10\cdot 0,1 \\
& {{p}_{r}}=13600\,Pa \\
\end{align}$
$\begin{align}
& {{p}_{a}}={{\rho }_{a}}\,g\,{{h}_{a}} \\
& {{p}_{a}}=1000\cdot 10\cdot 0,5 \\
& {{p}_{a}}=5000\,Pa \\
\end{align}$
$\begin{align}
& {{p}_{h}}={{p}_{r}}+{{p}_{a}} \\
& {{p}_{h}}=13600+5000 \\
& {{p}_{h}}=18600\,Pa \\
\end{align}$
$\begin{align}
& A=10\ c{{m}^{2}}={{10}^{-3}}{{m}^{2}} \\
& {{h}_{r}}=10\ cm=0,1\ m \\
& {{h}_{a}}=50\ cm=0,5\ m \\
& {{\rho }_{a}}=1{gr}/{c{{m}^{3}}}\;=1{000\ kg}/{{{m}^{3}}}\; \\
& {{\rho }_{r}}=13,6{gr}/{c{{m}^{3}}}\;=13{600\ kg}/{{{m}^{3}}}\; \\
\end{align}$
$\begin{align}
& {{p}_{r}}={{\rho }_{r}}\,g\,{{h}_{r}} \\
& {{p}_{r}}=13600\cdot 10\cdot 0,1 \\
& {{p}_{r}}=13600\,Pa \\
\end{align}$
$\begin{align}
& {{p}_{a}}={{\rho }_{a}}\,g\,{{h}_{a}} \\
& {{p}_{a}}=1000\cdot 10\cdot 0,5 \\
& {{p}_{a}}=5000\,Pa \\
\end{align}$
$\begin{align}
& {{p}_{h}}={{p}_{r}}+{{p}_{a}} \\
& {{p}_{h}}=13600+5000 \\
& {{p}_{h}}=18600\,Pa \\
\end{align}$
2. Konsep Hukum Pascal
Ilmuan Prancis, Blasie Pascal, menyatakan bahwa jika fluida berada dalam ruang tertutup, kemudian diberikan tekanan eksternal, maka tekanan tersebut akan didistribusikan ke seluruh titik dalam fluida tersebut. Pernyataan tersebut dikenal sebagai Hukum Pascal (Pascal’s Principle). Hasil pemikiran Pascal tersebut diterapkan dalam beberapa bidang teknologi, salah satunya adalah pompa hidrolik.Dalam sistem pompa hidrolik di atas, fluida berbentuk bejana berhubungan dengan sistem input dan output dengan luas penampang yang berbeda. Sesuai dengan prinsip Pascal, jika fluida tersebut diberikan tekanan input ${{p}_{in}}$, dengan gaya ${{F}_{in}}$, maka tekanan tersebut akan diteruskan ke penampang output $\left( {{A}_{out}} \right)$dengan besar tekanan yang sama $\left( {{p}_{in}}={{p}_{out}} \right)$. Sehingga pada penampang output akan menghasilkan gaya output ${{F}_{out}}$. Konsep tersebut jika dinyatakan dalam bentuk matematik adalah sebagai berikut:
$\begin{align}
& {{p}_{in}}={{p}_{out}} \\
& \frac{{{F}_{in}}}{{{A}_{in}}}=\frac{{{F}_{out}}}{{{A}_{out}}}\ldots \ldots \ldots \ldots \ldots \left( 3 \right) \\
\end{align}$
Berdasarkan persamaan 3 di atas, kita dapat menyatakan bahwa gaya berbanding lurus dengan luas penampang. Jika ${{F}_{in}}$ yang kecil diberikan pada penampang input ${{A}_{in}}$ yang kecil pula, maka akan menghasilkan ${{F}_{out}}$ yang besar pada penampang output ${{A}_{out}}$ yang lebih besar. Nah, dari konsep tersebut pompa hidrolik dimanfaatkan untuk mengangkat beban yang besar hanya dengan gaya kecil. Perbandingan $\frac{{{F}_{out}}}{{{F}_{in}}}$ disebut sebagai keuntungan mekanik.
Contoh Soal Tekanan Hidrostatis
Sebuah dongkrak hidrolik mempunyai pengisap kecil dengan diameter 10 cm dan pengisap besar dengan diameter 40 cm. Jika dongkrak tersebut di gunakan untuk mengangkat beban seberat 5.000 N, berapa gaya minimum yang harus di berikan kepada pengisap kecil?
Jawab:
$\begin{align}
& {{d}_{1}}=10\ cm \\
& {{d}_{2}}=40\ cm \\
& {{F}_{2}}=5000\ N \\
& {{F}_{1}}=\ ? \\
\end{align}$
$\begin{align}
& \frac{{{F}_{1}}}{{{A}_{1}}}=\frac{{{F}_{2}}}{{{A}_{2}}} \\
& \frac{{{F}_{1}}}{{\scriptstyle{}^{1}/{}_{4}}\pi {{d}_{1}}^{2}}=\frac{{{F}_{2}}}{{\scriptstyle{}^{1}/{}_{4}}\pi {{d}_{2}}^{2}} \\
& \frac{{{F}_{1}}}{{{d}_{1}}^{2}}=\frac{{{F}_{2}}}{{{d}_{2}}^{2}} \\
& \frac{{{F}_{1}}}{{{\left( 0,1 \right)}^{2}}}=\frac{5000}{{{\left( 0,4 \right)}^{2}}} \\
& {{F}_{1}}=312,5\ N \\
\end{align}$
Jadi gaya minimum yang diperlukan adalah 312,5 N.
$\begin{align}
& {{d}_{1}}=10\ cm \\
& {{d}_{2}}=40\ cm \\
& {{F}_{2}}=5000\ N \\
& {{F}_{1}}=\ ? \\
\end{align}$
$\begin{align}
& \frac{{{F}_{1}}}{{{A}_{1}}}=\frac{{{F}_{2}}}{{{A}_{2}}} \\
& \frac{{{F}_{1}}}{{\scriptstyle{}^{1}/{}_{4}}\pi {{d}_{1}}^{2}}=\frac{{{F}_{2}}}{{\scriptstyle{}^{1}/{}_{4}}\pi {{d}_{2}}^{2}} \\
& \frac{{{F}_{1}}}{{{d}_{1}}^{2}}=\frac{{{F}_{2}}}{{{d}_{2}}^{2}} \\
& \frac{{{F}_{1}}}{{{\left( 0,1 \right)}^{2}}}=\frac{5000}{{{\left( 0,4 \right)}^{2}}} \\
& {{F}_{1}}=312,5\ N \\
\end{align}$
Jadi gaya minimum yang diperlukan adalah 312,5 N.
3. Konsep Hukum Archimedes tentang Gaya Apung
Sekarang coba kita pelajari bersama tentang respon fluida terhadap benda yang ad di dalamnya. Ilustrasi berikut ini menunjukkan respon fluida terhadap benda, yaitu berupa gaya-gaya akibat tekanan fluida hidrostatis.Penampang atas benda yang berada pada kedalaman ${{h}_{1}}$ mendapatkan tekanan sebesar ${{p}_{1}}$ sehingga ada gaya ${{F}_{1}}$ ke arah bawah terhadap penampang atas benda. Begitu pula terjadi pada penampang benda bagian bawah. Pada penampang bawah benda yang berada di kedalaman ${{h}_{2}}$, fluida memberikan tekanan hidrostatis sebesar ${{p}_{2}}$ sehingga benda mendapatkan gaya ${{F}_{2}}$ ke atas. Nah, selisih antara ${{F}_{2}}$ dan ${{F}_{1}}$ merupakan gaya apung fluida ${{F}_{A}}$ yang diberikan pada benda. Secara matematis, konsep tersebut dijelaskan sebagai berikut:
$\begin{align}
& {{F}_{A}}={{F}_{2}}-{{F}_{1}} \\
& {{F}_{A}}={{p}_{2}}-{{p}_{1}} \\
& {{F}_{A}}=\left( {{\rho }_{f}}\ g\ {{h}_{2}} \right)A-\left( {{\rho }_{f}}\ g\ {{h}_{1}} \right)A \\
& {{F}_{A}}={{\rho }_{f}}\ g\ A\left( {{h}_{2}}-{{h}_{1}} \right) \\
& {{F}_{A}}={{\rho }_{f}}\ V\ g\ \ldots \ldots \ldots \ldots \ldots \left( 4 \right) \\
\end{align}$
Persamaan 4 merupakan besar gaya apung ${{F}_{A}}$ yang diberikan oleh fluida bermassa jenis ${{\rho }_{f}}$ kepada benda. Nah karena nilai ${{\rho }_{f}}\ V={{m}_{f}}$ yang merupakan massa fluida, maka:
$\begin{align}
& {{F}_{A}}={{\rho }_{f}}\ V\ g \\
& {{F}_{A}}={{m}_{f}}\ g \\
& {{F}_{A}}={{w}_{f}}\ \ldots \ldots \ldots \ldots \ldots \left( 5 \right) \\
\end{align}$
Berdasarkan persamaan 5, dapat disimpulkan bahwa besar gaya apung ${{F}_{A}}$ sama dengan berat fluida ${{w}_{f}}$ (bisa zat cair atau gas) yang dipindahkan akibat masuknya benda ke dalam fluida. Artinya, jumlah volume fluida yang dipindahkan $\left( V \right)$ sama dengan volume benda yang tercelup di dalam fluida. Konsep ini dinyatakan oleh ilmuan yang bernama Archimedes, dan disebut sebagai Hukum Archimedes.
Contoh Soal Hukum Archimedes – Gaya Apung
(1). Sebuah mahkota jika ditimbang di udara memiliki berat 25 N. Jika dimasukkan ke dalam air beratnya menjadi 15 N. Bila massa jenis air adalah 1000 kg/m3 dan percepatan gravitasinya 10 m/s2 maka massa jenis mahkota adalah ...
Jawab:
Berat benda di dalam fluida $w'$ akan berkurang dari berat benda di udara $w$ akibat adanya gaya apung ${{F}_{A}}$.
$\begin{align}
& w'-w={{F}_{A}} \\
& 25-15={{\rho }_{f}}\ V\ g \\
& 10=1000\cdot \ V\ \cdot 10 \\
& V={{10}^{-3}}\ {{m}^{3}} \\
\end{align}$
$\begin{align}
& {{\rho }_{benda}}=\frac{{{m}_{benda}}}{{{V}_{benda}}} \\
& {{\rho }_{benda}}=\frac{{25}/{10}\;}{{{10}^{-3}}} \\
& {{\rho }_{benda}}=2500\ {kg}/{{{m}^{3}}}\; \\
\end{align}$ dengan nilai ${{m}_{benda}}=\frac{w}{g}$ dan ${{V}_{benda}}={{V}_{fluida\ yang\ dipindahkan}}$
Berat benda di dalam fluida $w'$ akan berkurang dari berat benda di udara $w$ akibat adanya gaya apung ${{F}_{A}}$.
$\begin{align}
& w'-w={{F}_{A}} \\
& 25-15={{\rho }_{f}}\ V\ g \\
& 10=1000\cdot \ V\ \cdot 10 \\
& V={{10}^{-3}}\ {{m}^{3}} \\
\end{align}$
$\begin{align}
& {{\rho }_{benda}}=\frac{{{m}_{benda}}}{{{V}_{benda}}} \\
& {{\rho }_{benda}}=\frac{{25}/{10}\;}{{{10}^{-3}}} \\
& {{\rho }_{benda}}=2500\ {kg}/{{{m}^{3}}}\; \\
\end{align}$ dengan nilai ${{m}_{benda}}=\frac{w}{g}$ dan ${{V}_{benda}}={{V}_{fluida\ yang\ dipindahkan}}$
(2). Sebuah kubus terbuat dari kayu mempunyai sisi 10 cm dan mengapung di atas permukaan cairan. Jika massa jenis cairan 1,2 g/cm3. Hitunglah
a) Tinggi kubus yang berada di bawah permukaan cairan jika massa jenis kayu 0,8 g/cm3
b) Besar gaya ke atas yang di alami kubus kayu tersebut
Jawab:
a) Sesuai kesetimbangan Newton, besar gaya apung sama dengan berat benda
$\begin{align}
& {{F}_{A}}=w \\
& {{\rho }_{f}}\ g\ V={{m}_{b}}\ g \\
& {{\rho }_{f}}\ V={{\rho }_{b}}\ {{V}_{b}}\ \\
& {{\rho }_{f}}\ \left( A\ {{h}_{f}} \right)={{\rho }_{b}}\ \left( A\ h \right) \\
& {{\rho }_{f}}\ {{h}_{f}}={{\rho }_{b}}\ h \\
& 1,2\cdot {{h}_{f}}=0,8\cdot 10 \\
& {{h}_{f}}=\frac{20}{3}\ cm \\
\end{align}$
b) Besar gaya apung adalah
$\begin{align}
& {{F}_{A}}={{\rho }_{f}}\ g\left( A\ {{h}_{f}} \right) \\
& {{F}_{A}}=800\frac{kg}{{{m}^{3}}}\ \cdot 10\frac{m}{{{s}^{2}}}\left( {{\left( 0,1\ m \right)}^{2}}\cdot \frac{0,2}{3}\ m \right) \\
& {{F}_{A}}=\frac{16}{3}N \\
\end{align}$
a) Sesuai kesetimbangan Newton, besar gaya apung sama dengan berat benda
$\begin{align}
& {{F}_{A}}=w \\
& {{\rho }_{f}}\ g\ V={{m}_{b}}\ g \\
& {{\rho }_{f}}\ V={{\rho }_{b}}\ {{V}_{b}}\ \\
& {{\rho }_{f}}\ \left( A\ {{h}_{f}} \right)={{\rho }_{b}}\ \left( A\ h \right) \\
& {{\rho }_{f}}\ {{h}_{f}}={{\rho }_{b}}\ h \\
& 1,2\cdot {{h}_{f}}=0,8\cdot 10 \\
& {{h}_{f}}=\frac{20}{3}\ cm \\
\end{align}$
b) Besar gaya apung adalah
$\begin{align}
& {{F}_{A}}={{\rho }_{f}}\ g\left( A\ {{h}_{f}} \right) \\
& {{F}_{A}}=800\frac{kg}{{{m}^{3}}}\ \cdot 10\frac{m}{{{s}^{2}}}\left( {{\left( 0,1\ m \right)}^{2}}\cdot \frac{0,2}{3}\ m \right) \\
& {{F}_{A}}=\frac{16}{3}N \\
\end{align}$